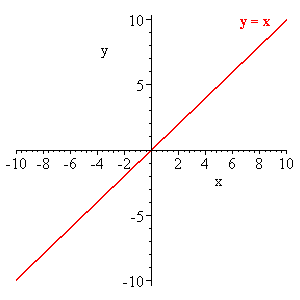
|
|
||
A standard function is one defined on an interval of that is obtained by a finite sequence of standard operations starting from any combination of three basic functions .
What are the basic functions ?
The identity function
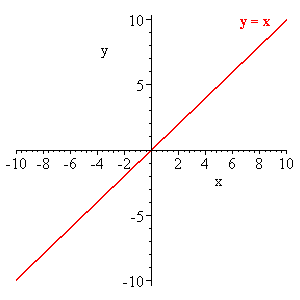
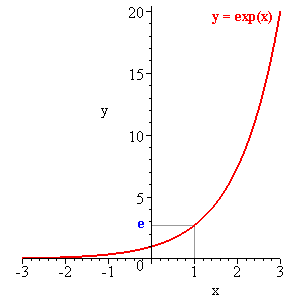
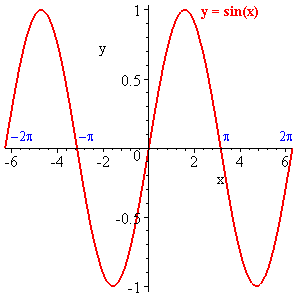
The sine function
What are the standard operations?
Multiplication by a number in , addition, subtraction, multiplication, division, substitution of the value of one function as argument of another, and taking the "inverse".
Most of the functions we encounter will be standard functions.
Examples: , , .
You can enter your favorite standard functions, and , in the following applet, and observe the effects of combining and in various ways, and also look at the inverse function to .
Note that when f has the same value for more than one argument, you must decide which of these arguments you want to call the value of the inverse function.
|
|