The mouse makes the vector x move. At the same time the graph shows Ax, in color and also moving. The green circle appearing is the unit circle and the red oval is its image under the action of the matrix. The are traced as you vary the vector x.
Possibly Ax is ahead of x. Possibly Ax is behind x. Sometimes Ax is parallel to x. At that parallel moment, Ax=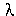 x and x is an eigenvector. x and x is an eigenvector.
The eigenvalue 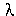 comes from the length and direction of Ax. Depending on your choices of the matrix A, the applet will demonstrate various possibilities. comes from the length and direction of Ax. Depending on your choices of the matrix A, the applet will demonstrate various possibilities.
1. There are no (real) eigenvectors. The directions of x and Ax never meet. The eigenvalues and eigenvectors are complex.
2. There is only one line of eigenvectors. The moving directions of x and Ax meet but don't cross.
3. There are eigenvectors in two independent directions. This is typical! Ax crosses x at the first eigenvector, and it crosses back at the second eigenvector.
Suppose A is singular (rank one). Its column space is a line. The vector Ax can't move around, it has to stay on that line. One eigenvector x is along the line. Another eigenvector appears when Ax = 0. Zero is an eigenvalue of a singular matrix.
You can follow x and Ax for these matrices. How many eigenvectors and where? When does Ax go clockwise instead of counterclockwise?
A=([0, -1], [1, 0])
A=([3, 0], [0, 3])
A=([1, 3], [1, 0]) (defective)
A=([1, 2], [2, 1])
|