Sub-navigation links

VIEW ALL COURSES

Document Distance: Problem Definition

Problem Definition | Data Sets | Programs: v1 - v2 - v3 - v4 - v5 - v6 | Programs Using Dictionaries

Let D be a text document (e.g. the complete works of William Shakespeare).

A word is a consecutive sequence of alphanumeric characters, such as "Hamlet" or "2007". We'll treat all upper-case letters as if they are lower-case, so that "Hamlet" and "hamlet" are the same word. Words end at a non-alphanumeric character, so "can't" contains two words: "can" and "t".

The word frequency distribution of a document D is a mapping from words $w$ to their frequency count, which we'll denote as $D (w)$ .

We can view the frequency distribution $D$ as vector, with one component per possible word. Each component will be a non-negative integer (possibly zero).

The norm of this vector is defined in the usual way:
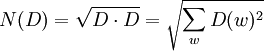$N(D) = \sqrt{D\cdot D} = \sqrt{\sum_w D(w)^2}$ .

The inner-product between two vectors $D$ and $D'$ is defined as usual.
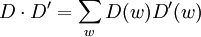$D\cdot D' = \sum_w D(w)D'(w)$ .

Finally, the angle between two vectors $D$ and $D'$ is defined:
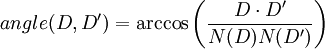
$angle(D,D') = \arccos\left(\frac{D\cdot D'}{N(D)N(D')}\right)$

This angle (in radians) will be a number between $0$ and 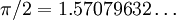$\pi/2 = 1.57079632\ldots$ since the vectors are non-negative in each component. Clearly,

$a n g l e (D, D) = 0.0$
for all vectors $D$ , and
$a n g l e (D, D') = p / 2$
if $D$ and $D'$ have no words in common.

Example: The angle between the documents "To be or not to be" and "Doubt truth to be a liar" is
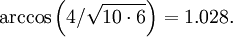
$\arccos{\left(4/\sqrt{10\cdot 6}\right)} = 1.028 .$

We define the distance between two documents to be the angle between their word frequency vectors.

The document distance problem is thus the problem of computing the distance between two given text documents.

An instance of the document distance problem is the pair of input text documents.