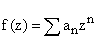
|
Home | 18.013A | Chapter 30 |
||
|
|
||
Suppose we have a function f(z) that is non singular in a unit circle around the origin. It will then have a power series expansion of the form
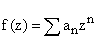
which will have radius of convergence at least 1.
If we look at this function on the unit circle, on which ![]() this series takes the form
this series takes the form 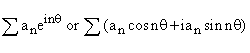 ,
so that if we define
,
so that if we define ![]() we have
we have
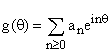
A series of this kind, or alternatively, a series of either of the forms
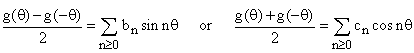
is called a Fourier series.
The series on the right in each case is periodic with period 2![]() .
.
By adding a constant factor in the arguments of the exponents sines or cosines
you can create Fourier series with other periods as well (replacing for example
![]() you can make the period L).
you can make the period L).
The coefficients an here can be determined by use of the integral formulae of the last section.
Integrating over the unit circle in z we can integrate ![]() to get
to get
![]()
The comparable formulae for bn and cn are
![]()
and
![]()
Exercise 30.14 Verify the correctness of these formulae by finding the b's
and c's for ![]()
Fourier series representations of functions are very useful for several reasons.
First, cosines and exponentials are easy to differentiate. Expressing a function as a sum of exponential functions is in effect expressing it as a sum of eigenfunctions of the derivative operator. This is the analog of using a basis in an ordinary vector space whose members are all eigenvectors of some important linear transformation on that space.
Second, if your analyze the response of an oscillator (or similar system) to external forcing at fixed frequencies, you can, by finding the Fourier series (or sometimes the Fourier transform, which is a similar thing for non-periodic functions) of your actual forcing function, you can find the response of your system to your actual forcing function.
You will learn more about this when you study differential equations.
Obviously Fourier series do not exist for all functions ![]() and need not for those that are singular in the range of integration.
and need not for those that are singular in the range of integration.
Also, since ![]() is an even function of
is an even function of ![]() for all n values and
for all n values and ![]() is an odd function of it, sine and cosine series are, as given here, appropriate
for odd and even functions g respectively.
is an odd function of it, sine and cosine series are, as given here, appropriate
for odd and even functions g respectively.
You can apply the formulae for the coefficients to any function, including
a discontinuous one like a step function, that for example, is ![]() for angles such that x > 0 and
for angles such that x > 0 and ![]() otherwise.
otherwise.
All sines and cosines are continuous, so that the partial sums of the Fourier series for a step function must be continuous. This means they must each be quite wrong in some interval around a point of discontinuity. Such intervals will typically shrink as the index of the partial sum increases.
If we integrate f multiplied by its complex conjugate around the unit circle, and its Fourier Series converges to it almost everywhere, the integral, should equal the sum of the terms gotten by substituting the series into the integral for g and its complex conjugate.
All cross terms among the series in the latter give 0 contribution, and we get, after substituting the series for g
![]()
Since the terms in the series on the right here are all positive, its partial sums must all be less than either of the two integrals on the left.
Mathematicians have devoted an enormous amount of effort to understanding when Fourier series converge.
Exercises:
30.15 Derive a similar result for the sine and cosine series.
30.16 Calculate the Fourier coefficients of the step function that is ![]()
30.17 Apply the equation just claimed above to this sequence of coefficients. What do you find?
|
|