|
Home | 18.013A | Chapter 1 | Section 1.2 |
||
|
|
||
Is countable?
Solution:
Each rational number in is a numerator in divided by a denominator in . It is characterized then by the pair such that . If we look at all pairs for in and in , we will actually get every over and over again, as
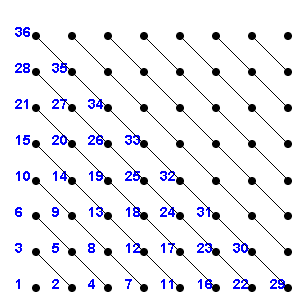
Therefore if we can list all the pairs for in and in we can get a list of the elements of by throwing away duplicates on this list.
Imagine then that we have a vertical column for each in and that column consists of a list of the elements of (as in Exercise 1.1). We can list the resulting pairs by going up every diagonal as in the illustration below. This will give a list of every pair for in and in .
You run through the elements of much faster than you do the elements of but again nobody cares about this fact.
To be explicit, we order the elements of our array in increasing order of and for fixed in increasing order of .
Thus the first few ratios in this order are
The first of these has then there are two with , three with , and so on.
The ratio will then appear as the ratio in the position on the list.
You can enter any ratio below and see where it occurs on the list and vice versa.

|
|