 |
Deduce from these two equations that for log to any base
we have log a * b = log a + log b.
Solution:
Suppose we want to prove this for logarithms to base c. We
deduced in the previous exercise that we can write 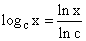 . .
Applying this fact to each logarithm here, the result we want
to prove is the same result for natural logs, with each term
divided by ln c.
In other words, the corresponding result for natural logarithms,
which we proved in the previous exercise, implies this one
on dividing each term by ln c, and using the fact just mentioned.
|
 |