|
The distance between two vectors v and w is
the length of the difference vector v - w.
There are many different distance functions that you will
encounter in the world. We here use “Euclidean Distance” in
which we have the Pythagorean theorem.
If the concepts of distance and length are used without additional
description this is what we will mean:
The square of the length of a vector w is the sum of
the squares (or more generally the sum of the absolute values
of the squares, when the components are complex numbers) of
its components. It is the dot product (w, w) (or w w).
But that is not the only distance you will see.
What properties should a length have?
It should be positive, and zero for the zero vector.
It should obey the triangle inequality: the length of the
sum of two vectors is no greater than the sum of their lengths.
It is nice if distance 0 means at the same place but not essential.
What other distances are in use?
Manhattan distance: length = sum of absolute values of components.
Hamming distance: length is number of non-zero components.
Length is Maximum component absolute value.
Suppose we call the components xi, and a small
quantity of any of them dxi, and the resulting
value of distance with components dxi let us call
ds.
Then in Euclidean space we have  .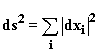
We define the metric  .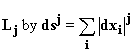
Euclidean space is then L2.
Exercise 3.14 Which values of j in the definition of Lj
correspond to Hamming, Manhattan, and Maximum component
size? (hints: j can be infinite; also for Hamming distance
the notions are similar but not exactly the same, and only
similar in a limit)
Length in Euclidean space when non-rectilinear coordinates
are used.
This is not a Euclidean vector space in general; for example
in polar coordinates, the usual rules of addition in a vector
space: the components of a sum are the sums of the components
does not hold in polar coordinates; because the angles and
lengths of the sum of two vectors are not the sums of their
individual angles and lengths.
In polar coordinates the r and directions are perpendicular,
and length in the r direction is as in the x direction; but
 does
not directly define length. The distance around a circle is
not 2 ,
but rather is 2r.
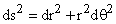As a result we get  as
we shall see.
Length in non-orthonal coordinates
Any k linearly independent k-vectors may be used as a
basis: Any other k-vector can be expressed as a linear combination
of them. (Why? By exercise 3.11 any other k-vector is in a
linear dependence with them which can be solved for that k-vector
in terms of the basis)
Thus, in two dimensions, for example, any two vectors
a and b with different directions can form a
basis and any vector v can be described by coordinates that
are the coefficients of these two: if v = s a
+ t b then we can describe v by the 2-vector (s, t).
However, if we are describing Euclidean space and the vectors
a and b are not orthogonal the length of v squared will not
be s2 + t2.. In general though, if we
define (s, t) to be v’, we get length squared is <v’|G|v’>
for some matrix G which depends on the angle between a
and b.
Thus, if a and b are unit vectors at angle
the matrix G is
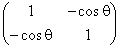
The matrix G is called the metric tensor for the given basis.
Different metrics: Minkowski space:
There are even vector spaces in which the concept of distance
is replaced by something that can be positive or negative:
such is Minkowski space: it has four dimensions, three spatial
and also time. In it the analog of distance is described by
ds2 = dx2 + dy2
+ dz2 –c2dt2
Vectors with s2 positive or negative are said
to be space-like or time-like respectively; those with s2
are said to lie on the “light cone”?
Why does anyone bother with such things? Linear changes
in the coordinates in Euclidean space that have the property
that they do not alter distances (so that the distance between
two points remains after the changes exactly what it was before),
are rotations in space. Similar changes in Minkowski space
are symmetries of Maxwell’s equations of electrodynamics,
and correspond to both rotations in space and ”Lorentz transformations”.
|
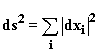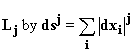