 |
In two dimensional space there is a simple formula for the
area of a parallelogram bounded by vectors v and
w with v = (a, b) and w = (c, d): namely
 ad
- bc ad
- bc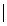
Why?
1. The statement that the area of a parallelogram with
sides given by the vectors (a, b) and (c, d) is |ad - bc|
is obviously true if b and c are 0, since the parallelogram
is then a rectangle with sides |a| and |d|, whose area is
|ad|.
2. Neither the area nor ad - bc changes
if we add a multiple of (a, b) to (c, d) or vice versa.
The parallelogram merely tilts, its base and altitude remain
the same. If we for example, add a to c, we get a change in
ad - bc of -ba; but adding b to d produces a compensating
change of ab to it, and the net effect is 0.
3. By repeatedly adding such multiples we can force b and
c to be 0, after which the statement holds.
4. Since these addings didn't change anything, it must have
been true at the beginning.
The combination ad - bc is called the determinant
of the matrix:
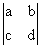
Given three vectors in three dimensions we can
form a 3 by 3 matrix of their components, and the absolute
value of the determinant of that matrix will be the volume
of the parallelepiped whose edges are determined by the three
vectors. In fact an analogous results holds for k k-vectors
†and determinants and the k-volume of the figure they bound.
What then is the determinant of a matrix?
In any dimension, it is defined
as follows:
1. it is linear in the elements of any row (or column)† so
that multiplying everything in that row by z multiplies the
determinant by z, and the determinant with row v +
w †is the sum of the determinants otherwise identical
with that row being v and that row being w.
2. It changes sign if two of its rows are interchanged (it
must therefore be 0 if two rows are identical).
3. The matrix with 1ís on the diagonal and 0ís elsewhere has
determinant 1.
The determinant is generally written as det M or as | M |
or sometimes || M ||.
If v and w are two rows of the matrix M we can
deduce from the first two conditions that adding a multiple
of v to w does not change the determinant of
M.
The volume of a parallelepiped bounded by edges whose
directions and lengths are that of u, v and w
is almost linear in u, v and w; it differs from
linearity only in that it is always positive, like length
in one dimension is. It is 1 if the vectors have unit length
and are mutually perpendicular, and does not change if one
side is added to another; The absolute value of the determinant
of the matrix formed by the components of the three vectors
obeys the same conditions and is therefore the same thing.
In higher dimensions the analog of volume
is called hypervolume and the same conclusion can be drawn
by the same argument: The hypervolume of the parallel sided
region determined by k vectors in k dimensions is the absolute
value of the determinant whose entries are their components
in the directions of the (orthonormal) basis vectors.
In fact, the determinant can be considered
a linear and signed version of hypervolume.
Consider the hypervolume of a parallel-sided region with sides
xA,B,C,... as a function of x. It is linear in x for positive
or negative x, but it is always positive, and its graph looks
like a V, taking the value 0 for x = 0.
The determinant is the same as the hypervolume for positive
or negative x and minus the hypervolume for the other, and
is therefore linear as a function of x.
|
 |
