|
This section is extremely sketchy. For further discussion
see Chapter 32.
Evaluating Determinants Gaussian elimination: To do
this you add multiples of one row to another until all entries
below the main diagonal are 0. The determinant is then the
product of the diagonal entries. Machines can do such things
for n by n matrices with n in the hundreds or thousands, but
people find the exercise a bit dull.
Expansion of a determinant in a row or column;
Let the matrix M have elements mij. Ihe first index
describes the row number, the second the column number.
Its determinant is a sum of the elements of any single row
each multiplied by a factor. What factor? For the jth element
of the ith row it is the determinant of the matrix obtained
by removing that row and column, multiplied by a sign factor
of -1 to the sum of the indices of the element, i + j:
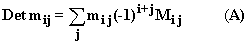
where Mij is the determinant of the matrix
obtained from M by eliminating its ith row and jth column.
Notice that we also have
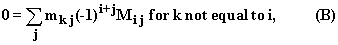
since this is the determinant of a matrix with two of its
rows equal to the kth row of M.
|
