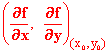» Required Reading » Table of Contents » Chapter 6 6.6 The Gradient and Directional Derivatives
	Previous Section	Next Section

We have seen above that the two dimensional vector

is called the gradient of f at argument (x₀, y₀). It is generally written as grad f orf.
The gradient appears in the equation for the tangent plane to the surface defined by f at (x₀, y₀):

From this equation we can deduce that a normal to this tangent plane is in the direction in the three dimensional ((x, y f L) space of (grad f, -1). The projection of this normal into the (x, y) plane is the vector grad f itself. This tells us:
Grad f is in the direction of the projection of the normal to the tangent plane to f at (x₀, y₀) into the (x, y) plane.
This relationship can be seen in the applet below.

The symbol is called "del". It is a strange thing called a vector operator. By itself it makes about as much sense as the noise of one hand clapping. But put next to something that the derivatives in it can act on, it makes perfect sense.

The equation for the linear approximation f L to f at (x₀, y₀) allows us to compute the directional derivatives of f at that point. Suppose we seek the directional derivative in a direction defined by unit vector u. Then if (r - r₀) = su, the directional derivative of f (which is also the directional derivative of its linear approximation, f L also) in that direction is the derivative of f L with respect to s:

But we have

so that f L's derivative with respect to s, the directional derivative of f in the direction of u, is given by .

If we have instead a function f of more variables, say x, y, z, t, ... we can use exactly the same discussion to describe changes, the only difference being that the tangent plane becomes the tangent hyperplane, and there are partial derivatives in more directions. The conclusions are exactly the same:

1. The gradient vector is in the direction of the projection of the normal to the tangent hyperplane into the hyperplane of coordinates.

2. The directional derivative in any direction is given by the dot product of a unit vector in that direction with the gradient vector.

3. The component of the gradient vector in the direction of any axis is the partial derivative of f with respect to the corresponding distance variable in that direction.

4. That partial derivative is the ordinary derivative with respect to that variable assuming all the other variables remain constant.