 |
Do things get more complicated in higher dimensions?
Not really. Here is a question that is about as complicated
as things get:
Suppose we are interested in the temperature T of a body that
is moving through ordinary space.
T in space is a function of position (x, y, z) and time t:
T = T(x, y, z, t) (we use the same letter to describe both
time and temperature to maximize confusion in what otherwise
would be a bald and unconvincing narrative.)
Now suppose further that the body in question has a trajectory
through space described by equations x = x(t), y = y(t) z
= z(t). (you might want to abbreviate this as r = r(t)
with r = (x, y, z). We raise the question, what is
the derivative with respect to time of the temperature experienced
by that body?
We write dT out in terms of differentials:
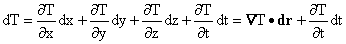
We also have
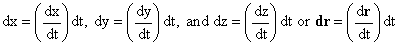
Putting these together we get
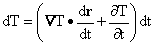
from which we conclude:
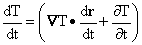
It is not a bad idea to realize whenever you encounter a
formula that looks like this that it undoubtedly arises from
an analogous situation, when a function depends on time and
also upon spatial variables that themselves depend on time.
This kind of thing is sort of a generalized chain rule and
is sometimes referred to as such. Please notice that the way
to handle any and all problems of this kind is to consider
differentials, include in their relations to one another all
possible dependencies, and relate them all to the differential
of the independent variable, here t. You can then divide the
differentials to find the derivative.
|
 |
