» Required Reading » Table of Contents » Chapter 9 9.1 Derivatives of Vector Functions; the Divergence
	Chapter Index	Next Section

The gradient is a vector function of several variables. Such an entity is called a vector field, and we can ask, how do we compute derivatives of such things?
We will consider this question in three dimensions, where we can answer it as follows.
Since a vector in three dimensions has three components, and each of these will have partial derivatives in each of three directions, there are actually nine partial derivatives of a vector field in any coordinate system.
Thus in our usual rectangular coordinates we have, with a vector field v(x, y, z), partial derivatives .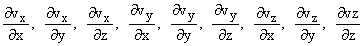
All of these can be computed by the same rules for computing partial derivatives of scalar functions (often called scalar fields). Fortunately for us, there are only two combinations of these that we usually encounter and that are worth knowing about.
The first of these is the divergence, written as div v, or in terms of the differential operator del, 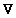which is the vector operator with components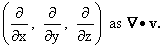
Explicitly, it is the dot product of this differential operator with the vector v:

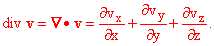
This is how the divergence is defined, and again it can be calculated by straightforward differentiation, but we must also address the question: what does it mean? Why is it of interest to us? How can we use it? How can we compute it in other coordinate systems? We will defer the answer to these questions until we have discussed integration, since the answers are intimately related to that subject.
However we can use the rules of differentiation to deduce the following useful statements:
The divergence of the sum of two vectors is the sum of their individual divergences.
And the divergence of a function f multiplied by a vector v is given as follows:

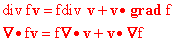
Exercises:

9.1 Derive this equation.

9.2 Apply it to find the divergence of 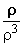in spherical coordinates. Recall that the vector 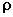has components (x, y, z) in spherical coordinates.