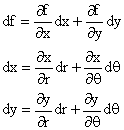|
Suppose we have a function given to us as f(x, y) in two
dimensions or as g(x, y, z).
In three dimensions, we can take the partial derivatives with
respect to the given variables and arrange them into a vector
function of the variables called the gradient of f, namely
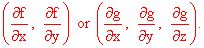
which mean
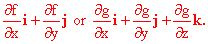
Suppose however, we are given f as a function of r and  ,
that is, in polar coordinates, or g in spherical coordinates,
as a function of ,
that is, in polar coordinates, or g in spherical coordinates,
as a function of  , ,
 ,
and ,
and 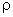 . .
For example, suppose f = 1 / r, or g = 1 /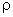 ,
or g = sin ,
or g = sin  . .
One way to find the gradient of such a function is to convert
r or 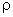 or
or  into rectangular coordinates using the appropriate formulae
for them, and perform the partial differentiation on the resulting
expressions.
into rectangular coordinates using the appropriate formulae
for them, and perform the partial differentiation on the resulting
expressions.
Thus we can write
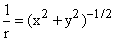
and find
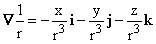
It is a bit more convenient to be able to express the gradient
directly in polar coordinates or spherical coordinates just
like we can do in our rectangular coordinates.
What does this entail? In our x and y coordinates we express
the gradient as a sum of a term, (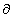 f
/ f
/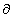 x),
times a unit vector in the x direction, namely i, and
a similar combination in the y direction, ( x),
times a unit vector in the x direction, namely i, and
a similar combination in the y direction, (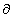 f
/ f
/  y)
j. In polar coordinates we want to express grad f as
something times a unit vector in the r-direction, plus something
else times a unit vector in the y)
j. In polar coordinates we want to express grad f as
something times a unit vector in the r-direction, plus something
else times a unit vector in the direction.
direction.
To do this we must address two questions: what are unit vectors
in the r and  directions? And what are the somethings these should be multiplied
by to give
directions? And what are the somethings these should be multiplied
by to give 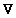 f? f?
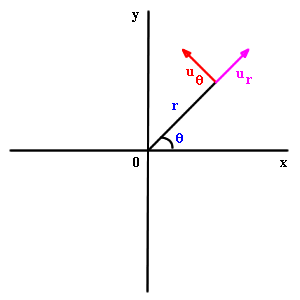
The first question has the following answers: the r direction
is the direction tilted by an angle  counterclockwise from the x axis. A unit vector in that direction,
call it ur, can be written in any of the
three following forms:
counterclockwise from the x axis. A unit vector in that direction,
call it ur, can be written in any of the
three following forms:
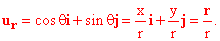
The unit vector in the  direction lies in the direction 90o past the r
direction and is therefore given by
direction lies in the direction 90o past the r
direction and is therefore given by
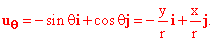
We can deduce how to write 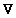 f
in polar coordinates directly in terms of these unit vectors
by using the following facts: f
in polar coordinates directly in terms of these unit vectors
by using the following facts:
First we know that if we make differential changes in r and
 the resulting change in f will be given by:
the resulting change in f will be given by:
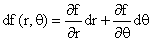 (A) (A)
Second, we want the change in f to obey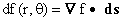 for any change in r and/or
for any change in r and/or where
ds is a vector pointing in the direction of the change
whose magnitude is the length of that change. where
ds is a vector pointing in the direction of the change
whose magnitude is the length of that change.
If we write 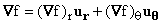 our task is to determine what the two coefficients here.
our task is to determine what the two coefficients here.
Suppose we change r by a distance dr without changing  .
Then by our equation (A) we have .
Then by our equation (A) we have 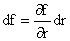 .
Since ds in the r direction is just .
Since ds in the r direction is just 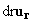 ,
we can write ,
we can write
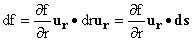
and we can identify 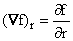 . .
In the  direction on the other hand, distance is given by rd
direction on the other hand, distance is given by rd ,
and the similar computation for changes in that direction
is ,
and the similar computation for changes in that direction
is
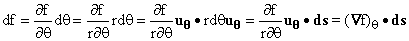
from which we can deduce: 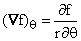 , ,
and we have shown:
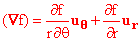 . .
A similar computation can be made for any orthogonal directions
in any dimension, and we can anticipate the result. The
component of  f
in the direction of any such variable will be the partial
derivative of f with respect to that variable, divided by
a factor which is the ratio of distance change in that direction
to change in the variable itself. f
in the direction of any such variable will be the partial
derivative of f with respect to that variable, divided by
a factor which is the ratio of distance change in that direction
to change in the variable itself.
Using this fact we can immediately deduce that the gradient
of  is
is 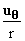 except
of course at r = 0 where except
of course at r = 0 where  is not differentiable. Similarly we find that the gradient
of
is not differentiable. Similarly we find that the gradient
of 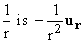 . .
Exercise 9.5 Find the gradient of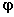 in spherical coordinates by this method.
in spherical coordinates by this method.
There is a third way to find the gradient in terms of given
coordinates, and that is by using the chain rule. We can first
consider differential change of f in rectangular coordinates,
and then relate the differential changes in x and y to differential
changes in the other coordinates, say r and  .
Combining these we can relate the change in f to changes in
the latter two variables. .
Combining these we can relate the change in f to changes in
the latter two variables.
Explicitly we can write
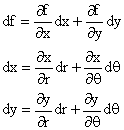
and use the latter two equations to get rid of dz and dy
in the first equation; the result is a rather messy expression
for df in terms of dr and d .
The gradient in polar coordinates can be deduced from this
expression, with the same answer as heretofore. This approach
is useful when f is given in rectangular coordinates but you
want to write the gradient in polar coordinates. .
The gradient in polar coordinates can be deduced from this
expression, with the same answer as heretofore. This approach
is useful when f is given in rectangular coordinates but you
want to write the gradient in polar coordinates.
This kind of substitution is sometimes called the chain
rule for partial derivatives.
It is worth noting that when we take the partial derivative
with respect to x or y we always mean that we are keeping
the other variable, y or x, constant; on the other hand the
partials with respect to r and  always mean keeping the other one of these,
always mean keeping the other one of these,  or r, constant.
or r, constant.
There are times and places where in a partial derivative
one can become confused as to which variable or variables
are being kept constant, and under such circumstances it is
wise to modify the notation to supply this information explicitly.
Thus we can write 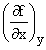 to mean the partial derivative with respect to x keeping y
fixed, and then there can be no confusion as to what is kept
constant.
to mean the partial derivative with respect to x keeping y
fixed, and then there can be no confusion as to what is kept
constant.
The facts to remember about the gradient are:
It is straightforward to compute, in any orthogonal coordinate
system You can use it to determine the directional derivative
of the function involved, in any direction. In rectangular
coordinates its components are the respective partial derivatives.
Of course the gradient of the sum of two fields is the sum
of their gradients (the gradient is a linear operator), and
the gradient of a product can be computed by applying the
usual product rule for differentiation.
|