|
The linear approximation to f is exactly
true if f ' is constant for that means that f is linear. The
inaccuracy of the linear approximation to f at x0 at
argument x arises from the changes to f ' between arguments
x0 and x. If f ' is differentiable in the interval
between x0 and x we can get a better approximation
to f at x by making a linear approximation to f ' and using
it to estimate the change to f in the interval. In short if
f ' is differentiable in that interval we can compute its
derivative, called the second derivative of f with respect
to x and written as f "(x) or as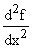 
or sometimes as  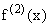and
use it to improve the estimate of f.
All of our standard functions have differentiable
derivatives and even differentiable second derivatives, etc
on forever wherever they are defined, except perhaps at specific
singular points. They are said to be “infinitely differentiable”
because we can keep differentiating them as long as we like.
We may therefore compute second derivatives, and also third
and higher derivatives and generate a sequence of better and
better approximations to any such function.
|
