 |
We now ask, how accurate are any
of the approximations here, from the trivial one, the constant
approximation f(x) = f(x0), the linear approximation,
etc.
Suppose x > x0 and m is them minimum value of
the kth derivative of f between these two arguments, and M
is the maximum value of that derivative there.
We will invoke a principle which in its simplest form is the
statement, the faster you move, the further you go, other
things being equal. Here we claim that if we invent a new
function fM by replacing the actual value of the
kth derivative of f throughout the interval (x0,
z) by its maximum value over that interval, then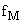 
and all its first k = 1 derivatives will obey 
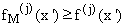for all x ' in that interval.
Think of it this way: if you increase speed (f ') to M you
increase the distance traveled. If alternately you increase
acceleration (f ") to M by the same argument that will
increase speed and hence will increase distance traveled.
And so on if you increase a higher derivative, that increase
will trickle down to increase all the lower derivatives and
ultimately f itself.
The nice thing about doing this is that the degree k approximation
to fM at x0 is exact at argument
x, because its kth derivative is constant in the interval
between them. Now the degree k approximation to fM
is the degree k-1 approximation to f plus  .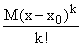
Our inequality above applied with j = 0 therefore tells us
that the k-1th approximation to f, plus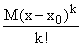
is at least f(x), while by the same argument applied in the
opposite order with M replaced by m, we can deduce that the
same approximation plus 
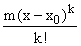is less than f(x).
The upshot of all this is have bounds on how far off the degree
k-1 approximation to f at x0 is from f at argument
x: their difference lies between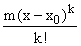
and .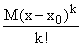
We can go one step further and notice that this tells us that
the error in the degree k-1 approximation can be
written as 
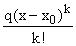where q lies between m and M. Since m and M are the minimum
and maximum values of f(k) between x0
and x, if f(k) takes on all values in between its maximum
and minimum (which it must if it is differentiable in that
interval) it will take on the value q. and we can write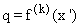 
for some x ' in that interval.
This allows us to translate our conclusion here into the following
statement.
Theorem:
The error in the degree k-1 approximation
to f at x0 evaluated at argument x is
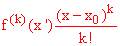
for some x ' in the interval
( x0, x).
Exercises:
10.5 State this theorem for k = 1. This result is called
"the mean value theorem".
10.6 Repeat the argument above for the situation that
occurs when x < x0. How does the conclusion
change? What is different in the argument?
|
|
