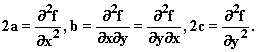» Required Reading » Table of Contents » Chapter 11 11.1 Quadratic Behavior in Two or More Dimensions
	Chapter Index	Next Section

Now let us consider what happens when f is a function of two variables, x and y.
We have seen that we can define partial derivatives directional derivatives and  differentiability in this case and in higher dimensions as well.

When it comes to quadratic and higher approximations, we can define them again without problem, but they are much more interesting, because quadratic functions of two or more variables are much more varied than those of one variable.

A general quadratic in two dimensions has the form ax² + bxy + cy² + dx + ey + g.
Such a function will have a critical point, at which its gradient is the 0 vector, where 2ax + by + d = 0 and bx + 2cy + e = 0 both hold.

If we call that point (x₀, y₀), we can write the quadratic function as in one dimension as a(x - x₀ )² + b(x - x₀)(y - y₀) + c(y - y₀)²  + g' so that the linear terms have been eliminated.

In two or more dimensions we define higher partial derivatives in the obvious way, the second partial derivative of f with respect to two variables is obtained by taking the first partial with respect to one and then taking the partial of that function with respect to the next.

The behavior of the quadratic  function here is, apart from a constant, captured by the coefficient a b and c, which are related to partial derivatives as follows:

Notice that if we make a matrix out of the four possible partial derivatives (two choices for first, with respect to x or y, and then the same two choices for second derivative) in the obvious way”:

the determinant of this matrix is the discriminant, of the quadratic, namely 4ac - b²

How does such a quadratic behave?
If a and c are both positive while b is 0 (behavior in each variable here looks like that of x² in one dimension and f will have a minimum at (x₀, y₀)).

If we reverse all signs making a and c negative, the quadratic will have a maximum at this point.