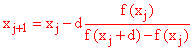» Required Reading » Table of Contents » Chapter 13 13.2 Poor Man's Newton
	Previous Section	Next Section

To apply Newton’s method as just described, it is necessary to differentiate the function f at each successive guess. This is not difficult, but requires a small amount of effort. We can instead apply what is essentially the same method, using an approximation to f '(x_i) of the form for some d. We then have to decide what to use for d, but with a spread sheet we can pick a small value to begin with and let it slowly go to zero as we iterate. If we wanted to be fancier, we could use a symmetric approximation to the derivative: .
How do we do all this? In box e2 we can put our initial value of d, say 10^(-3); then we can put "= e2*9/10" in e3 and copy it down, so that d will slowly decline to 0. (why slowly? If you go too fast round-off error might ruin you before you find your solution). The iteration here is

We can therefore put our guess in f2, put "= e2+f2"in g2, set h2 to "= f(f2)", copy it into i2  and then set f3 to "= f2-e2*h2/(i2-h2)", and copy g2, h2, i2 and e3 and f3 down, and we are done.

Exercise 13.7 Do this for the functions considered above. Do you find a difference between the results here and with the regular Newton method? If so, what?