|
A curve C in three dimensions can be defined by two equations
(that is as the intersection of two surfaces) or by use of
a single parameter as in two dimensions.
If q is an extreme values of F on C we cannot have 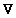 F F t
non-zero at argument q, by our general principle; otherwise
F will be larger on one side of q and smaller on the other
than its value at q. t
non-zero at argument q, by our general principle; otherwise
F will be larger on one side of q and smaller on the other
than its value at q.
The implications of this condition are different here however.
We can no longer say that 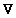 F
points in some particular direction at an extremal point.
Rather it must be normal to some particular direction, that
of the tangent vector to C at such points. F
points in some particular direction at an extremal point.
Rather it must be normal to some particular direction, that
of the tangent vector to C at such points.
When C is described by two equations, G = 0 and H = 0, t
is in the direction of 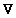 G G
 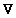 H,
and the statement that H,
and the statement that 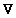 F
has no component in that direction is the statement that F
has no component in that direction is the statement that 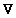 F
lies in the plane of F
lies in the plane of  G
and G
and  H
and so the volume of their parallelepiped is 0 and the
determinant whose columns are all these grads must be 0. H
and so the volume of their parallelepiped is 0 and the
determinant whose columns are all these grads must be 0.
Another way to state the same condition is to use two Lagrange
Multipliers, say c and d: and write
 F
= c F
= c  G
+ d G
+ d  H.
We can solve the three equations obtained by writing all three
components of this vector equation and use them to solve for
c, d and one more variable, which is in general all that you
need to locate the extremal points on the curve. H.
We can solve the three equations obtained by writing all three
components of this vector equation and use them to solve for
c, d and one more variable, which is in general all that you
need to locate the extremal points on the curve.
|
