» Required Reading » Table of Contents » Chapter 15 15.2 Intrinsic Properties of a Curve
	Previous Section	Next Section

First, what are they? What are the intrinsic local properties of the curve?
A straight line has a direction which we can describe by a unit vector in that direction: Thus the equations x = 2t, y = 3t, z = t describe a line that has the direction of the vector (2, 3, 1)  and of the unit vector .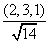
A general differentiable curve is one that looks like a straight line when looked at over a sufficiently short interval. Thus at any point it has a slope and that slope will in general be in the direction of the vector 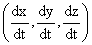, which we will call v(t). We define T(t) to be a unit vector in the direction of v(t):

.

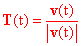We define one more parameter s(t) which represents the distance along the curve  between some origin point on the curve and where you are on it at argument t.
The intrinsic information about the curve is contained in the relation between T(t) and s(t), between the tangent vector and the distance parameter along the curve.

To a first approximation, the curve at any point is characterized by its slope there, which is the direction of T(t) or T(t(s)).