» Required Reading » Table of Contents » Chapter 16 16.1 Constant Force
	Chapter Index	Next Section

The simplest physical example of a situation with such a force is the motion of an object on the surface of the earth subject to the pull ot the earth’s gravity.
When the acceleration is constant and is given by -gk, we can deduce that the velocity, v(t), of the object whose derivative this acceleration must be  will obey:

v(t) = v(t₀) - g(t - t₀)k,

 and this velocity is the derivative of a position vector r(t) which must take the form:

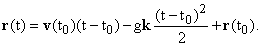
We have not discussed at this point how we deduce these things, but we can verify them by differentiating r and v, and checking their correctness at time t₀.
(In general, if the acceleration were given to us as a polynomial function of t, we could produce forms like these containing polynomials of degree one and two greater than that of the acceleration to describe velocity and position vectors, and adjust their coefficients to yield correct formulae for them. However, physical phenomena are rarely described by forces and hence accelerations that depend explicitly on time. Rather the most important and fundamental situation is one in which the object experiences a force that depends linearly on its position.)
Though these equations provide a complete solution to the problem of motion in three dimensions subject to a constant acceleration, they do not provide convenient answers to all the questions we might raise about the situation. Thus, we can use them to determine r and v at any time t, but they are not particularly convenient for deducing what r is as a function of v, or vice versa.
To help answer such questions, we define the Energy function, E by

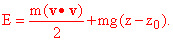
The first of these terms is called the kinetic energy, T, of the object, and the second its potential energy, V. The force experienced by the object can be written here as -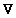V; the derivative of E with respect to time is then given by

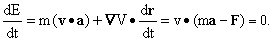
This fact, called the conservation of energy,  holds whenever F can be written as a gradient. Here if we know the value of E at any time, we can use this fact to compute z as a function of v or vice versa from the expression above for E.