 |
If we want to study an unknown function defined by some physical
or other situation, the method of analysis consists of studying
its derivative, as a function of appropriate variables, and
deducing from them an equation for it. This will generally
be an example of a differential equation, which is an equation
that involves derivatives of an unknown function. The process
of solving a differential equation is called integrating it.
One important special case of this problem occurs when we
have an explicit formula for the derivative of a function
f defined over an interval of a single variable x and this
formula is depends only on the independent variable x. We
want to know as much as this information can provide us about
the function f.
Thus we want to go from g(x), with 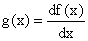 for
a < x <b, to f(x); we want to undo the differential
operator  ,
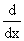and this could be called undifferentiating to find f(x) itself
or as much about it as we can; the standard name for this
task is finding the anti-derivative of g(x).
This procedure is also called finding the indefinite integral
of g(x) with respect to x. We will not use this terminology
below, because we want to define the definite integral
in a completely different way, and want to avoid confusion
between the two notions. Of course you can anticipate from
the similarity in names that there will be an intimate relation
between the definite integral (here not defined at
all) and the anti-derivative here. If you guess as
much you are right.
|
|
