 |
Are there functions that are not Riemann integrable? Yes there are, and you
must beware of assuming that a function is integrable without looking at it. The
simplest examples of non-integrable functions are: x-1 in the interval
[0, b]; and x-2 in any interval containing 0. These are intrinsically
not integrable, because the area that their integral would represent is infinite.
There are others as well, for which integrability fails because the integrand
jumps around too much. An extreme example of this is the function that is 1 on
any rational number and 0 elsewhere. Thus the area chosen to represent a single
interval in a Riemann sum will be either its width or 0 depending upon whether
we pick a rational x or not at which to evaluate our integrand in that interval.
No matter how small the intervals are, you can have a Riemann sum of 0 or of b-a.
In this case it is possible to use a cleverer definition of the area to define
it. (You can argue, in essence, that there are so many more irrational points
than rational ones, you can ignore the latter, and the integral will be 0 )
If we consider the area under the curve defined by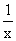 
in an interval between -a and b for positive a and b, the area has an infinite
positive part between 0 and b and an infinite negative part between -a and 0.
It is possible to define the area here so that these cancel out and meaning can
be given to the net area. (If you leave out the interval between -d and d for
any small d, the remaining area is finite, and can be computed. You can then take
the limit of this area as d goes to 0. The result is called the principle part
of the integral and can be and is so defined for functions like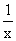
whose infinite areas can have opposite signs and can counterbalance each other)
|
|
