 |
When given an integral defined over area, the standard procedure for reducing
it to ordinary integral it is to make it into a multiple integral. A multiple
integral is an expression involving two or more ordinary integrals, in which the
limits of integration on one may depend on the values of the variables of integration
of the next, so that the integrals may have to be performed in a specific order.
Here are some examples:
To reduce an area integral to a pair of multiple integrals you must perform
the following steps
1. Choose a set of variables that is convenient to you. This can include rectangular
variables or polar coordinates or anything else. You choose them to make either
the integrand, or the limits of integration that will be required (preferably
both) as simple as possible; and choose an order in which you intend to define
the integration in these variables. When you have no clue you can start with the
obvious variables x and y.
2. Express the limits of integration appropriately so that the area you are integrating
over is represented by the points within your limits of integration.
3. Express the element of area dA in terms of your variables u and v and du and
dv.
4. Express the integrand in terms of your variables.
5. Integrate each of the ordinary integrals you have produced, if necessary in
the appropriate order.
Example: Suppose we wish to integrate the function exp(-r2)
over the entire xy plane.
One way to do this is with ordinary x y coordinates.
(The limits of integration are then from 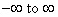 in
each variable. This is an improper integral as the limits are infinite, and we
have really defined integrals only over finite regions. However the integrand
here is so well behaved for large values of any variables here that we can ignore
this fact and imagine that we cut off the integrals at huge finite values. This
will not change the answer significantly). in
each variable. This is an improper integral as the limits are infinite, and we
have really defined integrals only over finite regions. However the integrand
here is so well behaved for large values of any variables here that we can ignore
this fact and imagine that we cut off the integrals at huge finite values. This
will not change the answer significantly).
The element of area dA is dxdy in rectangular coordinates.
The integrand can be expressed as exp(-x2-y2).
Our task then is to evaluate.
We can also perform this integration in polar coordinates
Here r goes from 0 to infinity, and  goes from 0 to 2
goes from 0 to 2 .
The area element is the product of the line elements dr and rd .
The area element is the product of the line elements dr and rd , so that we have dA = rdrd
, so that we have dA = rdrd .
The integrand is .
The integrand is 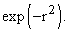
Here the  integration is trivial and yields the value 2
integration is trivial and yields the value 2 -
0 or just 2 -
0 or just 2 .
We are left with the integral from 0 to infinity of .
We are left with the integral from 0 to infinity of 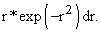 If we set
If we set 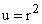 ,
we have du = 2rdr, and the integrand dr becomes ,
we have du = 2rdr, and the integrand dr becomes 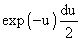 and the limits of integration on u are still 0 and infinity. The value of this
integral is therefore 1/2, and the product of the two integrals
and the limits of integration on u are still 0 and infinity. The value of this
integral is therefore 1/2, and the product of the two integrals
here is just  . .
Notice that we have just proven that the integral of 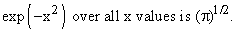
|
 |
