» Required Reading » Table of Contents » Chapter 30 30.3 Conditions for Absolute Convergence
	Previous Section	Next Section

The characteristic series whose behavior conveys the most information about the behavior of series in general is the geometric series. This is a power series in the variable x, and its terms are the powers of x:

G = 1 + x + x² + ... + xⁿ + ...

It has the nice property that if you subtract 1 from it, and divide by x you get it back again:

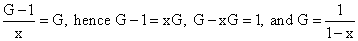
This series has the property that it is absolutely convergent for |x| < 1, and has a singularity when x is 1. The formula for it is infinite at x = 1, and the series itself becomes 1 + 1 + 1 + ..., which obviously diverges.

The most general method for determining whether a given series absolutely converges is called the Comparison test: you compare your series to another series. If that other series absolutely converges and each term in your series is smaller in absolute value than the corresponding term in it, then your series will also converge absolutely.
Likewise, if the other series is not absolutely convergent, and each term in yours is larger in absolute value than the corresponding term in the other, then your series will diverge as well.

The geometric series provides a basic comparison series for this test. Since it converges for x < 1, we may conclude that a series for which the ratio of successive terms 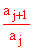is always at most x for some x value with x < 1, will absolutely converge. This statement defines the ratio test for absolute convergence.
It is also clear that when the ratio of successive terms just given always exceeds 1 then the series will not converge absolutely.

From now on let us assume that all the terms in our sequence are positive. (This neither helps nor hurts absolute convergence.) With this assumption we can talk about ordinary convergence and we are actually talking about absolute convergence.

The interesting problem occurs when the ratio of successive terms approaches 1 as n increases, or when it fluctuates around 1. The harmonic series provides a good example of such a sequence.
Since its nth term is 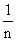, the ratio of successive terms is 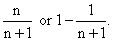This is NOT small enough for convergence, since this series diverges.
Here is an easy way to see that it diverges. Notice that after the first term, there is one more term that is 1/2 or larger (namely the second term), two more that are 1/4 larger, four more that are 1/8 or larger, eight more that are 1/16^th or larger and so on. In general, doubling the length of a partial sequence from n to 2n provides n new terms each of size at least 1/2n, so it increases the partial sum by at least 1/2. The sum going on forever is therefore unbounded.

We can determine what happens to the partial sums of this series up to the n^th term as n increases by comparing partial sums to an integral. Here is how.
We can represent the sum of the first n terms of any sequence of positive elements by a histogram, the element a_j corresponding to a rectangle of width 1 and height a_j located between j-1 and j on the x axis.
The coordinates of the top right hand side of each rectangle are (j, a_j) which here are (j, 1/j). The coordinates of the left hand top of each rectangle are similarly (j-1,1/j)
Now let us consider the integral from 1 to n of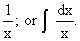
This integration can be performed and the answer is ln(n). The curve of 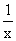obviously lies above the histogram of the n-1 terms of this series after the first one. We can conclude that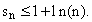
On the other hand the left hand endpoints of the rectangles all meet the curve 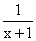. And that the region under the curve carried from 0 to n-1 lies entirely within the rectangles, from the first to the n-1st. But the integral from x = 0 to n-1 of 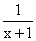is the same as the integral from x = 1 to n of 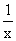and is ln(n).
So we may deduce

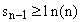
and therefore,

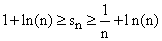
As n increases, ln(n) goes to infinity. We have therefore shown that the harmonic series diverges, but its partial sums differ by an amount on the order of 1/2 from ln(n).

Exercise 30.4 The difference between sn and ln(n) is called Euler's constant and is denoted by the Greek letter gamma, 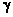. Use a spreadsheet to find the first 128 partial sums of this series, compare the partial sums, s₁, s₂, s₄, s₈, ..., s₁₂₈. Use extrapolation to eliminate differences between these that go down as factors of 2, 4, 16, 64, etc. Use these to estimate .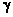

This approach to determining convergence can be applied similarly to any series whose terms decrease. It is called the integral test. The function that meets the upper left hand corners of the rectangles in the histogram will lie under it, and the function that meets the upper right hand corners will lie above it, after its first term, so that convergence of the series is equivalent to convergence of the integral of the corresponding function.

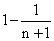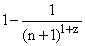It is clear from this example, that decline by a factor of term to term is insufficient for convergence of a positive sequence. On the other hand, this integral test shows that decline by a factor of for any positive z is sufficient for convergence, since a corresponding integral will converge.

Exercise 30.5 Verify this claim.