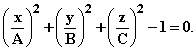| |
|||||
To do this you must first decide on an order in which you wish to perform the integrals. There are circumstances in which this does not matter much, and those in which the difference in the ease of doing the integral is very substantial. However, you can always decide to change the order of integration if you are dissatisfied with your choice. So suppose we have an area integral and we wish to integrate over the variable
x first and then y. Under some circumstances the limits on x involve different curves for different
y values. You must choose your x integration accordingly. All this undoubtedly sounds vague and frighteningly difficult. In fact, if you draw a picture, it is usually very easy to do. Without a picture it is indeed frighteningly difficult to get it right. We consider some examples. There is an x interval to integrate over for all y values between 0 and 1.
Suppose you want to integrate over the triangle between y = x, y = 0 and x
= 1.
Exercises:31.1 Suppose you want to integrate over this same triangular region integrating y first and then x. What are the appropriate limits in that case? 31.2 Suppose instead we wish to integrate over x from y to 2, and then over
y from y = 0 to 1. This defines a trapezoid. What are the limits of integration
if we want to integrate over y first? 1. The area bounded by x = 1, x = 2, y = x and y = 0. This is simple if you
integrate over y first. But if you integrate over x first you find the integral
must be split into two parts. 2. The area bounded by It should be clear from these examples that without an adequate picture it is almost impossible to get these things right. Below is an applet for trying different limits in rectangular and polar coordinates. Try it on the examples above and on the following areas. Exercises: 31.3 Consider the interior of a circle of radius A centered about the origin.
What are the limits on x and y, or on r and 31.4 Find limits integrating on x first then y, and vice versa, for the area between y = x3, x = 1, x = 2 and y = -x3. 31.5 Find limits of integration for the ellipse with boundary
Integrating over a volume can be done in exactly the same way. You first
select an order of integration, on the basis of your guess of what will be most
convenient. You then create a picture of the region of integration, and determine
the intervals of integration starting from the last integration variable, working
back to the first. Consider integration over a sphere of radius A, whose bounding surface obeys
the equation Exercises: 31.6 Determine appropriate limits of integration if you wish to integrate
some integrand over an ellipsoid with boundary 31.7 Determine appropriate limits in rectangular and cylindric coordinates for the region inside a cone of with boundary z = 1 and z = r2. (The origin is the bottom tip of this region).
|
|||||||||||||||||||||||||||

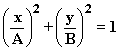 ,
what are other potential variables?
,
what are other potential variables?