» Required Reading » Table of Contents » Chapter 32 32.4 More on Determinants
	Previous Section	Next Section

We have defined the determinant of a matrix to be a linear function of its rows or columns whose magnitude is the hypervolume of the region with edges given by its columns, or by its rows.
The determinant has a number of important properties as follows:

1. Linearity in columns: If we have column n-vectors c(k) and d(k), for k = 1 to n, and pick any j in this range then the n dimensional determinant obeys the condition

det (c(1), …c(j - 1), a*c(j) + b*d(j), c(j + 1),…,c(n)) =

a*det (c(1), …c(j - 1), c(j), c(j + 1),...,c(n)) +

b*det (c(1), …c(j-1), d(j), c(j + 1),...,c(n)).

2. Linearity in rows: write this one out yourself.

3. The determinant is 0 if two columns are the same. (likewise for rows) Equivalently, it changes sign if you interchange two rows (or columns).

4. The determinant can be evaluated by a process like row reduction.

5. The determinant of the matrix product of two matrices is the product of their determinants.

6. In terms of the elements of a matrix M in any one column say M_1j, M_2j, ...
the determinant can be expressed as

det M = M_1j*C(1, j) + M_2j*C(2, j) + ...

The quantities C(i, j) that occur here are called cofactors of the matrix M. C(i, j) must be linear in all the rows of M except the i-th and in all the columns of M except the j-th, and it must be 0 if two of those rows or columns are the same; so it is proportional to the determinant of the matrix obtained by removing the i-th row and j-th column from M. The proportionality constant turns out to be (-1)^i+j.

7. The inverse of the matrix M is the matrix whose (i, j)-th element is .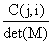

8. If you have a set of equations of the form Mv = c, then the i-th component of v is given by the ratio of the determinant of the matrix obtained by taking M and substituting c for the i-th column of M, divided by the determinant of M itself. (This statement is called Cramer's Rule)

9. The condition that the determinant of a matrix is 0 means that the hypervolume of the region determined by the columns is 0 which means that they are linearly dependent, and it means that there is a non-zero linear combination of the columns that is the zero vector. Which means that for this vector v, we have Mv = (0).

10. The determinant is unchanged by rotations of coordinates.

11. The polynomial of degree n in x defined by det(M - xI) is called the characteristic polynomial of M. Its roots (solutions to it = 0) are called the eigenvalues of M.

We now comment on these claims.
The first three follow immediately from the definition of the determinant as a linear version of hypervolume.

It follows from these that you can add a multiple of one row to another without changing the determinant: because by linearity the change would have to be a multiple of the determinant of a matrix with two identical rows. But then you can do this until the matrix is diagonal, at which point the determinant, again by linearity, is the product of the diagonal elements times the determinant of the identity matrix (which is 1).
The statement that the determinant of a product of two matrices is the product of the determinants is important and useful. It follows by these two observations:

1. If the matrix A is diagonal, then det A is the product of the diagonal elements of A. On the other hand, the rows of AB are just the rows of B each multiplied by the corresponding diagonal element of A. By linearity then, the determinant of AB is the product of the diagonal elements of A times the determinant of B, that is, it is the product of the determinant of A and that of B, as we have claimed.

2. If we apply row operations as just discussed on A to obtain a new matrix A' and apply the same row operation to (AB) to obtain (AB)' we will have
A'B = (AB)' and we will have det A = det A' , and det AB = det A'B.

We can do this until A is diagonal, at which point we can use the first remark to tell us that (det A') * det B = det A'B, from which our conclusion follows.

The statements about cofactors merely make explicit what it means to be linear in each row and column. The sign factor can be deduced from the fact that it is 1 if you consider the first row and column, (think of the identity matrix) and you can switch rows and columns with their neighbors i - 1 and j - 1 times to rearrange things so that the i-th row and j-th column become the first and everything else is in their original orders. This will cause i + j - 2 sign changes, which gives the sign factor noted.

As already noted somewhere the inverse statement is a statement about the dot products of the rows of the inverse with the columns of the original matrix. The diagonal products must be 1 which follows from the cofactor formula for the determinant, and the off diagonal ones must be zero because by that same formula they represent the determinants of matrices with two identical columns or rows.

Cramer's rule is the observation that by the definition of the inverse, the desired coefficient is the dot product of the i-th row of the inverse of M with the vector c. But by the cofactor formula this is dot product of the i-th column of the cofactor matrix with the vector c, divided by the determinant of M, and that is the ratio of the two determinants of Cramer's rule.