|
This system obeys the equation
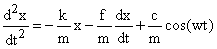
To set this up on a spreadsheet, I leave a place to enter the constants and
initial conditions in the first few rows; these are t0, x(t0),
x'(t0), m, k, f, c and w.
Then I would devote a column to each of t, x, x' and x", first entering
the initial conditions and then using the formulae above to obtain each new value
from the previous one.
I like to set the second t value to t0 + d, and then all subsequent
ones to twice the previous value minus the value two before 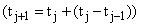 which
means that the intervals in t all have the same size. which
means that the intervals in t all have the same size.
The following chart shows how the setup might look on a spreadsheet:
|
Column A
|
Column B
|
Column C |
|
M=
|
1
|
|
|
k=
|
1
|
x0=
|
|
f=
|
0.3
|
u0=
|
|
d=
|
0.01
|
u'0=
|
|
c=
|
1
|
|
|
w=
|
1.5
|
|
| |
|
|
|
x
|
U
|
u'
|
|
=D3
|
=D4
|
=D5
|
|
=A10+B5
|
=B10+(A11-A10)*(C10+C11)/2
|
=C10+(A11-A10)*(D10+D11)/2
|
|
=2*A11-A10
|
=B11+(A12-A11)*(C11+C12)/2
|
=C11+(A12-A11)*(D11+D12)/2
|
|
=2*A12-A11
|
=B12+(A13-A12)*(C12+C13)/2
|
=C12+(A13-A12)*(D12+D13)/2
|
|
=2*A13-A12
|
=B13+(A14-A13)*(C13+C14)/2
|
=C13+(A14-A13)*(D13+D14)/2
|
|
=2*A14-A13
|
=B14+(A15-A14)*(C14+C15)/2
|
=C14+(A15-A14)*(D14+D15)/2
|
|
=2*A15-A14
|
=B15+(A16-A15)*(C15+C16)/2
|
=C15+(A16-A15)*(D15+D16)/2
|
|
=2*A16-A15
|
=B16+(A17-A16)*(C16+C17)/2
|
=C16+(A17-A16)*(D16+D17)/2
|
|
=2*A17-A16
|
=B17+(A18-A17)*(C17+C18)/2
|
=C17+(A18-A17)*(D17+D18)/2
|
|
=2*A18-A17
|
=B18+(A19-A18)*(C18+C19)/2
|
=C18+(A19-A18)*(D18+D19)/2
|
|
=2*A19-A18
|
=B19+(A20-A19)*(C19+C20)/2
|
=C19+(A20-A19)*(D19+D20)/2
|
|
=2*A20-A19
|
=B20+(A21-A20)*(C20+C21)/2
|
=C20+(A21-A20)*(D20+D21)/2
|
|
=2*A21-A20
|
=B21+(A22-A21)*(C21+C22)/2
|
=C21+(A22-A21)*(D21+D22)/2
|
|
=2*A22-A21
|
=B22+(A23-A22)*(C22+C23)/2
|
=C22+(A23-A22)*(D22+D23)/2
|
|
=2*A23-A22
|
=B23+(A24-A23)*(C23+C24)/2
|
=C23+(A24-A23)*(D23+D24)/2
|
|
=2*A24-A23
|
=B24+(A25-A24)*(C24+C25)/2
|
=C24+(A25-A24)*(D24+D25)/2
|
|
=2*A25-A24
|
=B25+(A26-A25)*(C25+C26)/2
|
=C25+(A26-A25)*(D25+D26)/2
|
|
=2*A26-A25
|
=B26+(A27-A26)*(C26+C27)/2
|
=C26+(A27-A26)*(D26+D27)/2
|
Column D is here:
| Column D |
|
0
|
|
1
|
|
0
|
| |
|
=MIN(B1000:B2000)
|
| |
|
u"
|
|
=(-$B$3*B10-$B$4*C10+$B$6*SIN($B$7*A10))/$B$2
|
|
=(-$B$3*(B10+(A11-A10)*C10)-$B$4*(C10+(A11-A10)*D10)-$B$6*SIN($B$7*A11))/$B$2
|
|
=(-$B$3*(B11+(A12-A11)*C11)-$B$4*(C11+(A12-A11)*D11)-$B$6*SIN($B$7*A12))/$B$2
|
|
=(-$B$3*(B12+(A13-A12)*C12)-$B$4*(C12+(A13-A12)*D12)-$B$6*SIN($B$7*A13))/$B$2
|
|
=(-$B$3*(B13+(A14-A13)*C13)-$B$4*(C13+(A14-A13)*D13)-$B$6*SIN($B$7*A14))/$B$2
|
|
=(-$B$3*(B14+(A15-A14)*C14)-$B$4*(C14+(A15-A14)*D14)-$B$6*SIN($B$7*A15))/$B$2
|
|
=(-$B$3*(B15+(A16-A15)*C15)-$B$4*(C15+(A16-A15)*D15)-$B$6*SIN($B$7*A16))/$B$2
|
|
=(-$B$3*(B16+(A17-A16)*C16)-$B$4*(C16+(A17-A16)*D16)-$B$6*SIN($B$7*A17))/$B$2
|
|
=(-$B$3*(B17+(A18-A17)*C17)-$B$4*(C17+(A18-A17)*D17)-$B$6*SIN($B$7*A18))/$B$2
|
|
=(-$B$3*(B18+(A19-A18)*C18)-$B$4*(C18+(A19-A18)*D18)-$B$6*SIN($B$7*A19))/$B$2
|
|
=(-$B$3*(B19+(A20-A19)*C19)-$B$4*(C19+(A20-A19)*D19)-$B$6*SIN($B$7*A20))/$B$2
|
|
=(-$B$3*(B20+(A21-A20)*C20)-$B$4*(C20+(A21-A20)*D20)-$B$6*SIN($B$7*A21))/$B$2
|
|
=(-$B$3*(B21+(A22-A21)*C21)-$B$4*(C21+(A22-A21)*D21)-$B$6*SIN($B$7*A22))/$B$2
|
|
=(-$B$3*(B22+(A23-A22)*C22)-$B$4*(C22+(A23-A22)*D22)-$B$6*SIN($B$7*A23))/$B$2
|
|
=(-$B$3*(B23+(A24-A23)*C23)-$B$4*(C23+(A24-A23)*D23)-$B$6*SIN($B$7*A24))/$B$2
|
|
=(-$B$3*(B24+(A25-A24)*C24)-$B$4*(C24+(A25-A24)*D24)-$B$6*SIN($B$7*A25))/$B$2
|
|
=(-$B$3*(B25+(A26-A25)*C25)-$B$4*(C25+(A26-A25)*D25)-$B$6*SIN($B$7*A26))/$B$2
|
|
=(-$B$3*(B26+(A27-A26)*C26)-$B$4*(C26+(A27-A26)*D26)-$B$6*SIN($B$7*A27))/$B$2
|
|
=(-$B$3*(B27+(A28-A27)*C27)-$B$4*(C27+(A28-A27)*D27)-$B$6*SIN($B$7*A28))/$B$2
|
|
=(-$B$3*(B28+(A29-A28)*C28)-$B$4*(C28+(A29-A28)*D28)-$B$6*SIN($B$7*A29))/$B$2
|
|
=(-$B$3*(B29+(A30-A29)*C29)-$B$4*(C29+(A30-A29)*D29)-$B$6*SIN($B$7*A30))/$B$2
|
The results look like this:
|
mu" = -ku-fu' -c sin wx
|
|
|
|
m=
|
1
|
|
|
|
k=
|
1
|
x0=
|
0
|
|
f=
|
0.3
|
u0=
|
1
|
|
d=
|
0.02
|
u'0=
|
0
|
|
c=
|
1
|
|
|
|
w=
|
1.5
|
min u in st state
|
-0.769651461
|
| |
1
|
|
|
|
x
|
u
|
u'
|
u"
|
|
0
|
1
|
0
|
-1
|
|
0.02
|
0.9997976
|
-0.020239955
|
-1.0239955
|
|
0.04
|
0.999185688
|
-0.040951318
|
-1.047140848
|
|
0.06
|
0.99815498
|
-0.062119497
|
-1.06967697
|
|
0.08
|
0.996696465
|
-0.083731975
|
-1.091570886
|
|
0.1
|
0.994801389
|
-0.105775593
|
-1.11279094
|
|
0.12
|
0.992461268
|
-0.128236563
|
-1.133306027
|
|
0.14
|
0.989667897
|
-0.15110048
|
-1.153085631
|
|
0.16
|
0.986413369
|
-0.174352335
|
-1.172099856
|
|
0.18
|
0.98269008
|
-0.197976528
|
-1.190319459
|
|
0.2
|
0.978490746
|
-0.221956881
|
-1.207715881
|
|
0.22
|
0.973808411
|
-0.246276653
|
-1.224261277
|
|
0.24
|
0.968636459
|
-0.270918551
|
-1.239928548
|
|
0.26
|
0.962968626
|
-0.29586475
|
-1.254691366
|
Using excel we can exhibit graphs by choosing x-y scatter plots of the first
three columns and of the second and third columns.
Realize that you can watch what happens as it happens when you vary parameters
if you do this.
Exercise 33.1 With k = m = 1 and c non-zero, locate the frequency w at which
the periodic steady state u amplitude is greatest for f = 0.1. (home in on it
by divide and conquer means.)
Do the same for k = 2, m = 1.
|
