Please note that animations A and B use an older Indeo video compression not supported by most multimedia players. If you have problems playing these files, we recommend using the VLC multimedia player.
The animations were generated with MATLAB software.
Directions: Click on the images to begin the animation.
A) Illustration of Total Derivative: Steady Temperature Field
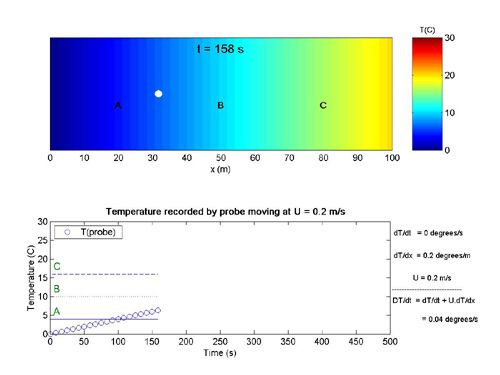
Illustration of total derivative: steady temperature field.
This animation shows a one-dimensional system with a spatial gradient of temperature, T(x). A temperature probe (white dot) moves with the flow, making a Lagrangian observation. The probe records the material (total) derivative. Go to the theory section (page 6) for some background material on the concept of the total derivative.
* Note to Unix users: the animation opens up behind active windows
B) Illustration of Total Derivative: Unsteady Temperature Field

Illustration of total derivative: unsteady temperature field.
This animation shows a one-dimensional system with an unsteady temperature field, T(x,t). A temperature probe is moving through the flow at velocity u, and it records the material derivative. Three additional probes are located at the fixed positions A, B, and C. Go to the theory section (page 6) for some background material on the concept of the total derivative.
* Note to Unix users: the animation opens up behind active windows
C) Steady, Spatially Accelerating Flow in a Pipe

Steady, spatially accelerating flow in a pipe.
In this animation, flow through a pipe accelerates downstream as the pipe cross-section decreases. The velocity and displacement of a probe moving with the flow are shown versus time. For some background and thought problems pertaining to this animation, review the theory (page 6) behind spatially accelerating flows.
* Note to Unix users: the animation opens up behind active windows.










