Course Description
Differential Equations are the language in which the laws of nature are expressed. Understanding properties of solutions of differential equations is fundamental to much of contemporary science and engineering. Ordinary differential equations (ODE’s) deal with functions of one variable, which can often be thought …
Differential Equations are the language in which the laws of nature are expressed. Understanding properties of solutions of differential equations is fundamental to much of contemporary science and engineering. Ordinary differential equations (ODE’s) deal with functions of one variable, which can often be thought of as time.
Course Info
Instructors
Departments
Learning Resource Types
theaters
Lecture Videos
laptop_windows
Simulations
notes
Lecture Notes
assignment_turned_in
Problem Sets with Solutions
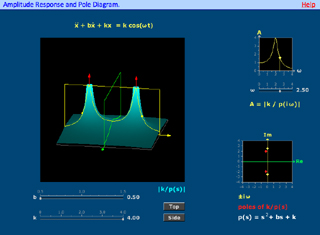
A spring system responds to being shaken by oscillating. When the input frequency is near a natural mode of the system, the amplitude is large. This can be understood in the frequency domain using the Laplace transform and its pole diagram. (Image courtesy Hu Hohn and Prof. Haynes Miller.)
