Lecture 10: Survey of Difficulties with Ax = b
Description
The subject of this lecture is the matrix equation \(Ax = b\). Solving for \(x\) presents a number of challenges that must be addressed when doing computations with large matrices.
Summary
Large condition number \(\Vert A \Vert \ \Vert A^{-1} \Vert\)
\(A\) is ill-conditioned and small errors are amplified.
Undetermined case \(m < n\) : typical of deep learning
Penalty method regularizes a singular problem.
Related chapter in textbook: Introduction to Chapter II
Instructor: Prof. Gilbert Strang
Problems for Lecture 10
From textbook Introduction Chapter 2
Problems 12 and 17 use four data points \(\boldsymbol{b}\) = (0, 8, 8, 20) to bring out the key ideas.
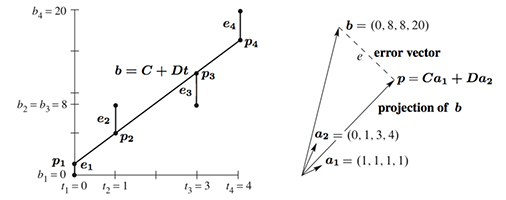
\(\hspace{10pt}\)Figure II.3: The closest line \(C + Dt\) in the \(t − b\) plane matches \(C\boldsymbol{a}_1 + D\boldsymbol{a}_2\) in R4.
12. With \(b\) = 0, 8, 8, 20 at \(t\) = 0, 1, 3, 4, set up and solve the normal equations \(A^{\mathtt{T}}A\widehat {\boldsymbol{x}} = A^{\mathtt{T}}\boldsymbol{b}\). For the best straight line in Figure II.3a, find its four heights \(p_i\) and four errors \(e_i\). What is the minimum squared error \(E=e^2_1+ e^2_2+e^2_3+e^2_4\) ?
17. Project \(\boldsymbol{b}\) = (0, 8, 8, 20) onto the line through \(\boldsymbol{a}\) = (1, 1, 1, 1). Find \(\widehat x = \boldsymbol{a}^{\mathtt{T}}\boldsymbol{b}/\boldsymbol{a}^{\mathtt{T}}\boldsymbol{a}\) and the projection \(\boldsymbol{p} = \widehat x \boldsymbol{a}\). Check that \(\boldsymbol{e} = \boldsymbol{b} − \boldsymbol{p}\) is perpendicular to \(\boldsymbol{a}\), and find the shortest distance \(\|\boldsymbol{e}\|\) from \(\boldsymbol{b}\) to the line through \(\boldsymbol{a}\).










