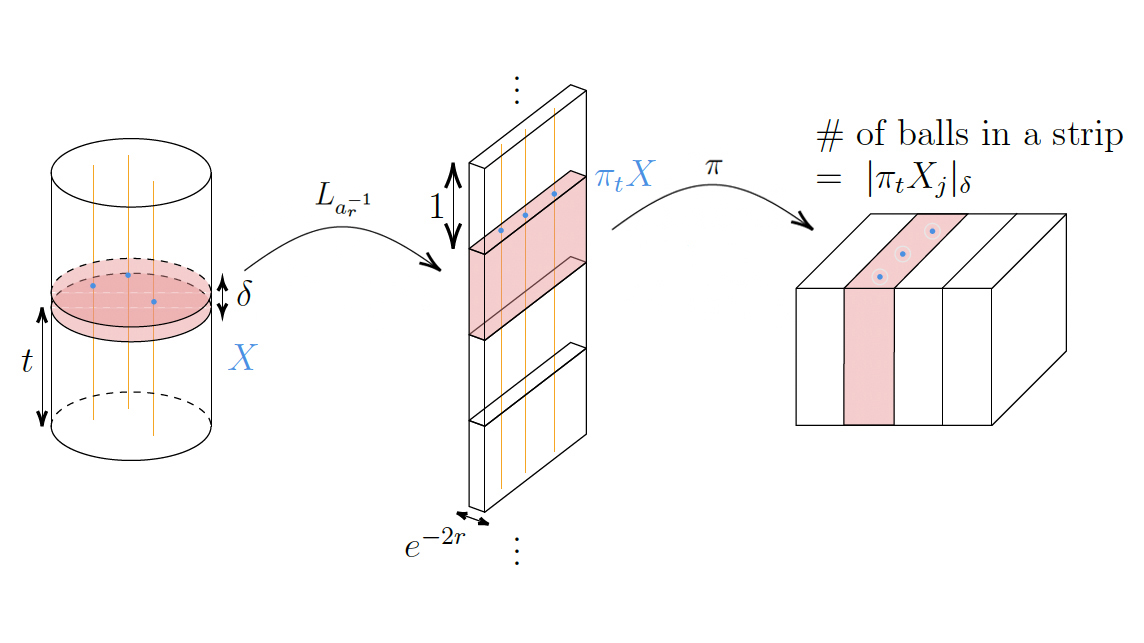
Course Description
The class studies projection theory, starting from the first questions and building up to recent developments. Projection theory studies how a set X behaves under different orthogonal projections. Questions of this type aren’t usually emphasized in the graduate analysis curriculum, but they come up in many areas …
The class studies projection theory, starting from the first questions and building up to recent developments. Projection theory studies how a set X behaves under different orthogonal projections. Questions of this type aren’t usually emphasized in the graduate analysis curriculum, but they come up in many areas of math, including harmonic analysis, analytic number theory, additive combinatorics, and homogeneous dynamics.
We will survey several applications of projection theory. For each topic, we will introduce and motivate the topic and see how it connects with projection theory. We will prove something about each topic but not necessarily the strongest results.
Course Info
Instructor
Departments
Learning Resource Types