Course Description
This course covers the classical partial differential equations of applied mathematics: diffusion, Laplace/Poisson, and wave equations. It also includes methods and tools for solving these PDEs, such as separation of variables, Fourier series and transforms, eigenvalue problems, and Green’s functions.
Course Info
Instructor
Departments
Learning Resource Types
grading
Exams with Solutions
notes
Lecture Notes
assignment
Problem Sets
Problem Set Solutions
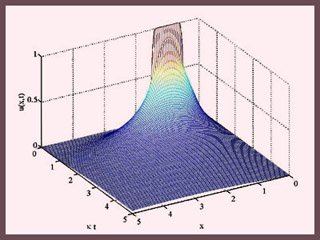
Time evolution of the temperature distribution u(x,t) on a semi-infinite rod whose end (at x=0) is kept at 0. Initially (t=0), the temperature of the rod is 1 between x=0.5 and x=1.5, and is zero everywhere else. (Image by Dr. Matthew Hancock.)










