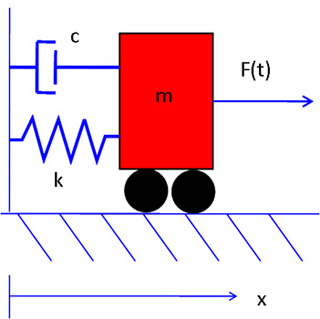
A moving cart attached to a wall by a spring and a dashpot. The equations of motion for every 1-degree-of-freedom system can be linearized around the equilibrium points to the second order differential equation that describes this system. Thus, understanding the free response and selected forced responses for this system can give deep insight into the stability of the equilibrium points and the behavior of a large number of systems. See Lectures 20 and 21 and Recitation 11 for more information. (Image courtesy of MIT OpenCourseWare.)