Course Description
This course presents the fundamental concepts of quantum mechanics: wave properties, uncertainty principles, the Schrödinger equation, and operator and matrix methods. Key topics include commutation rule definitions of scalar, vector, and spherical tensor operators; the Wigner-Eckart theorem; and 3j (Clebsch-Gordan) …
This course presents the fundamental concepts of quantum mechanics: wave properties, uncertainty principles, the Schrödinger equation, and operator and matrix methods. Key topics include commutation rule definitions of scalar, vector, and spherical tensor operators; the Wigner-Eckart theorem; and 3j (Clebsch-Gordan) coefficients. In addition, we deal with many-body systems, exemplified by many-electron atoms (“electronic structure”), anharmonically coupled harmonic oscillators (“intramolecular vibrational redistribution: IVR”), and periodic solids.
Course Info
Instructor
Departments
Learning Resource Types
grading
Exams with Solutions
notes
Lecture Notes
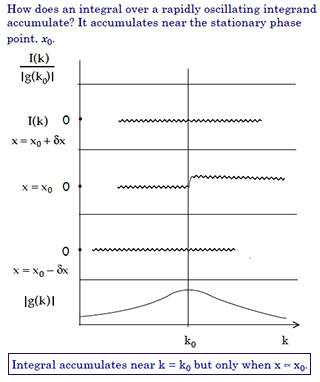
From Lecture #3 Notes: Learn how to determine the value of the integral without actually evaluating the integral. Amaze your friends!










