Course Description
Complex analysis is a basic tool with a great many practical applications to the solution of physical problems. It revolves around complex analytic functions—functions that have a complex derivative. Unlike calculus using real variables, the mere existence of a complex derivative has strong implications for the …
Complex analysis is a basic tool with a great many practical applications to the solution of physical problems. It revolves around complex analytic functions—functions that have a complex derivative. Unlike calculus using real variables, the mere existence of a complex derivative has strong implications for the properties of the function. Applications reviewed in this class include harmonic functions, two dimensional fluid flow, easy methods for computing (seemingly) hard integrals, Laplace transforms, and Fourier transforms with applications to engineering and physics.
Course Info
Instructor
Departments
Learning Resource Types
grading
Exams with Solutions
notes
Lecture Notes
Recitation Notes
assignment_turned_in
Problem Sets with Solutions
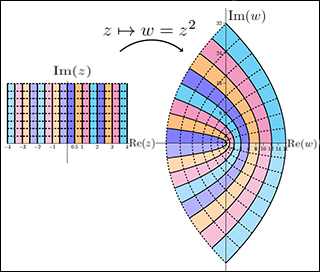
In the figure above, f(z) = z² maps the first two quadrants to the entire plane. (Image courtesy of Jeremy Orloff.)








