Course Description
This course will give a detailed introduction to the theory of tensor categories and review some of its connections to other subjects (with a focus on representation-theoretic applications). In particular, we will discuss categorifications of such notions from ring theory as: module, morphism of modules, Morita …
This course will give a detailed introduction to the theory of tensor categories and review some of its connections to other subjects (with a focus on representation-theoretic applications). In particular, we will discuss categorifications of such notions from ring theory as: module, morphism of modules, Morita equivalence of rings, commutative ring, the center of a ring, the centralizer of a subring, the double centralizer property, graded ring, etc.
Course Info
Instructor
Departments
Learning Resource Types
assignment
Problem Sets
notes
Lecture Notes
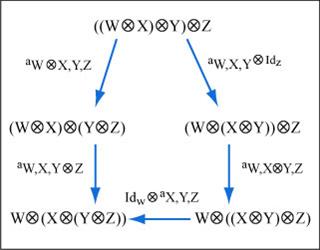
The pentagon axiom is commutative for all objects W, X, Y, Z, in C. (Image by MIT OpenCourseWare.)










