Course Description
This course is the continuation of 18.785 Number Theory I. It begins with an analysis of the quadratic case of Class Field Theory via Hilbert symbols, in order to give a more hands-on introduction to the ideas of Class Field Theory. More advanced topics in number theory are discussed in this course, such as Galois …
This course is the continuation of 18.785 Number Theory I. It begins with an analysis of the quadratic case of Class Field Theory via Hilbert symbols, in order to give a more hands-on introduction to the ideas of Class Field Theory. More advanced topics in number theory are discussed in this course, such as Galois cohomology, proofs of class field theory, modular forms and automorphic forms, Galois representations, and quadratic forms.
Course Info
Instructor
Departments
Learning Resource Types
notes
Lecture Notes
assignment
Problem Sets
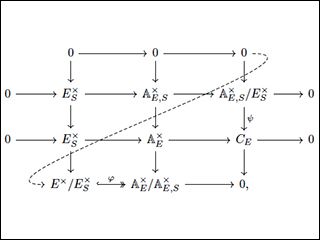
Commutative diagram: the map φ is surjective by the choice of S and is also injective by the definition of ESx. (Courtesy of Oron Propp. Used with permission.)








