Course Description
This is a course on the singular homology of topological spaces. Topics include: Singular homology, CW complexes, Homological algebra, Cohomology, and Poincare duality.
Course Info
Instructor
Departments
Topics
Learning Resource Types
assignment
Problem Sets
notes
Lecture Notes
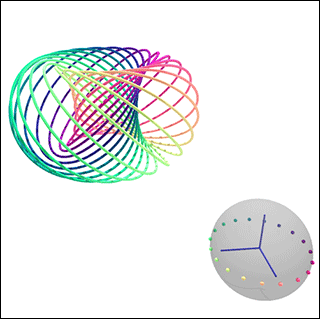
The Hopf fibration shows how the three-sphere can be built by a collection of circles arranged like points on a two-sphere. This is a frame from an animation of fibers in the Hopf fibration over various points on the two-sphere. (Image and animation courtesy of Niles Johnson.








