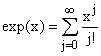» Required Reading » Table of Contents » Chapter 2 » Section 2.1 Exercise 2.1
	Back to Section 2.1	Next Exercise

Figure out the series for exp x  and prove it  to be so.

Solution:

The power series expansion of exp(x) about 0 has the form

exp(x) = a₀ + a₁ x + a₂ x² + ...

When x is near 0 exp(x) is near 1. This implies a₀ = 1.

The derivative of exp(x) is itself and so is also near 1 when x is near 0.

Differentiating the series we find

This allows us to identify a₁ = a₀, 2a₂ = a₁, 3a₃ = a₂, from the fact that the coefficients of each power of x must be the same here and in the previous expression for exp(x) and in general ja_j = a_j-1.

        This allows us to identify     We conclude that the series for exp(x) is the sum from j = 0 to infinity of  , which we write as: