|
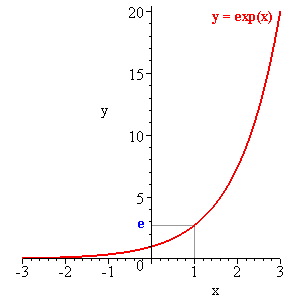
The exponential function, denoted by exp x, is defined
by two conditions:
Its value for argument 0 is 1.
And it is its own derivative. Comment
Which means its slope is 1 at 0 and it grows as x and hence
exp x increases, so that it increases faster and faster.
For negative values it never gets to be 0.
At any point x, the tangent line to the curve y = exp(x) hits
0 at x-1
We can find a series expansion
for exp x by using these conditions and the fact that 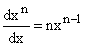 . .
What has derivative 1? x? 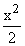 ?...? ?...?
Exercises:
2.1 Figure out the series for exp x and prove it to
be so. Solution
2.2 Set up a spreadsheet to compute it up to say the 100th
term using your series. Solution
2.3 For x = 1, how many terms do you need to get 10 place
accuracy? Solution
2.4 Choose a random x and compute (exp x)*(exp -x) with
a spreadsheet. What do you get? How about (exp 3x)*(exp –x)3?
Solution
The same kind of series solution can be obtained for any
function which is its own derivative or has derivative which
is a constant multiple say c of itself.
This allows us to prove the fundamental properties of the
exponential function.
These are expressions for exp (x + r) and for exp
rx.
The former has derivative itself but has value exp r when
x = 0; the latter has value 1 at x = 0, but has derivative
r times itself.
Both of these statements are immediate consequences of the
chain rule of differentiation.
Given a positive number a we can compute a^n for any integer
n by multiplying together n factors of a. We can define a^(1/n)
to be the inverse function to a^n. And we can define a^(m/n)
to be the product of m factors of a^(1/n). Thus we can define
a^r for any rational r. Can we define it for irrational r?
We can and will prove that for any rational power r that x^r
has derivative r(x^r)/x. Let us try to define it so that this
is its derivative for any r.
We can immediately deduce then that exp(x*r)
= (exp(x))^r.
Why?
1. The equation is true for x = 0, where it reads, 1 = 1.
2. The derivatives of the two sides are the same everywhere,
as you may compute using the chain rule.
Exercise 2.5 State and prove these fundamental properties
ie, expressions for exp (x + r) and for exp
rx. (hint: what value do they have at x = 0? What are their
derivatives? Deduce their series from these statements and
identify them.) Solution
Well I can't resist telling you that exp(a
* b) = (exp a)b. Because of this fact you
rarely see (exp a) written as we have written it here. We
define the constant 'e' to be exp(1) , and applying the equation
above we get exp b = exp 1 * b = eb 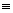 e^b.
e^b.
The expression ea is used 99% of the time to describe
(exp a). In fact, the main use of the notation (exp a) is
when it is inconvenient to use a superscript, as in typing,
or machine entry. Computers and spreadsheets use the notation
e^a which avoids superscripts but is ugly.
Logically the notation a^b or ab represents a concept
that we have not actually defined, except through our definition
of exp(b).
In fact, the statement exp(a*b) = (exp
(a))b can be taken as a definition of the
operation of "raising to a power" when acting on
exp (a).
|

