» Required Reading » Table of Contents » Chapter 2 » Section 2.3 Exercise 2.12
	Previous Exercise	Next Exercise

Set up a spreadsheet to compute the sin x for any inputted x. How many terms in the sin x power series expansion do you need to evaluate sin .5 to 8 decimal places?

Solution:

The power series expansion of sin x consists of the odd power terms in the expansion of exp x, with alternating signs,

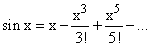
We can set up a spreadsheet to compute it in many ways, and here is one.

We will do almost the same thing as done for exp(x) in column A we will put j; and j will start at 1 and go up by 2 in each successive row. We will put x in the first row of column B and –x² in successive rows, and multiply previous C entry by entry in B and divide by entry in A and by entry in A, minus 1.   

We will get the following formulae in the spreadsheet

The numerical results will be:

You can see that the first 4 terms by themselves give sin .5 correctly to 8 decimal places.