|
The important properties are:
The Pythagorean theorem (which is really our definition of
distance as discussed below).
The addition theorems which are expressions for sin(a +
b) and cos (a + b).
The half angle theorem (a consequence of the previous two.)
All trigonometric functions depend only on the angle mod 2 .
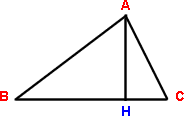
The law of sines: In the triangle ABC, the ratio of the length
AB and AC is the ratio of the sines of the opposite angles: .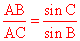
This is just the fact that both ABsin B and ACsin C are equal
to AH.
The law of cosines.(see next chapter)
The coordinates of the point on the unit circle at angle
t with center at the origin are(cos ,
sin)
which means y = sin,
x = cos.
The tangent line to a circle with center at the origin through
(x, y) is perpendicular to the line from the center to (x,
y) i and points toward the y axis in the first quadrant.
Its direction is given by (-sin,
cos)
All properties follow from the differential properties of
the sine.
For the moment we assume:
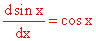
Then using
,
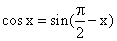We get
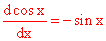
And we have cos 0 = 1
And so we have sin 0 = 0, (sin 0)’ = 1, (sin 0 )” = 0, (sin
0)”’ = -1 and further derivatives repeat as (from the start
0 1 0 -1 0 1 0 -1 0 1 0 -1, etc, at argument 0. This information
determines a power series formula for the sine of x.
What polynomial has derivative 1 at x = 0, and value 0 there?
When you realize that the monomial xk has all its
derivatives 0 at x = 0 except the kth which is k!, we can
read off the power series for sine from the sequence of derivative
values at 0.
We get
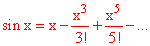
and similarly
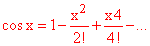
which implies
exp(ix) = cos x + i
sin x. (A)
We can therefore use the properties of the exponential function
to deduce the addition theorem for sines and cosines:
exp i(a+b) = cos (a
+ b) + i sin( a + b) = exp ia * exp ib
=
cos a cos b – sin a sin b + i(cos a sin b + cos b sin a)
Exercises:
2.10 Derive the formulae for sine x and cosine x in terms
of exp(ix) and exp(–ix), that follows from equation (A) above.
Solution
2.11 Find expressions for (sin t/2)2 and (cos
t/2)2 from the Pythagorean theorem and the cosine
addition theorem. Solution
2.12 Set up a spreadsheet to compute the sin x for any
inputted x. How many terms in the sin x power series expansion
do you need to evaluate sin .5 to 8 decimal places? Solution
|
