|
The volume of a parallelepiped with sides A, B
and C is the area of its base (say the parallelogram
with area |B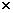 C|
) multiplied by its altitude, the component of A in
the direction of B C|
) multiplied by its altitude, the component of A in
the direction of B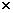 C.
This is the magnitude of A C.
This is the magnitude of A B B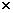 C;
but it is also the magnitude of the determinant of the matrix
with columns A, B and C, so these linear
functions of the vectors here are the same up to sign. The
usual sign convention gives: C;
but it is also the magnitude of the determinant of the matrix
with columns A, B and C, so these linear
functions of the vectors here are the same up to sign. The
usual sign convention gives:
A (B (B C)
= det(A, B, C) C)
= det(A, B, C)
This product is not changed by cyclically permuting the
vectors (for example to B, C, A) or by
reversing the order of the factors in the dot product.
We can deduce then that A B B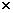 C
= C C
= C A A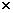 B
= A B
= A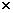 B B C.
In words, we can switch the dot and
cross product without changing anything in this entity. (in
either formula of course you must take the cross product first).
It changes sign, however if you just reverse the vectors in
the cross product. C.
In words, we can switch the dot and
cross product without changing anything in this entity. (in
either formula of course you must take the cross product first).
It changes sign, however if you just reverse the vectors in
the cross product.
The vector triple product, A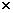 (B (B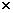 C)
is a vector, is normal to A and normal to B C)
is a vector, is normal to A and normal to B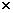 C
which means it is in the plane of B and C. And
it is linear in all three vectors. We can deduce it is a multiple
of B that is linear in A and C plus a
multiple of C that is linear in A and B,
with the condition that it is normal to A. Any multiple
of B(A C
which means it is in the plane of B and C. And
it is linear in all three vectors. We can deduce it is a multiple
of B that is linear in A and C plus a
multiple of C that is linear in A and B,
with the condition that it is normal to A. Any multiple
of B(A C)
- C(A C)
- C(A B)
will obey all these conditions. What multiple is it? Earlier
we saw that the square of the area of a parallelogram with
sides A and B can be written either as (A B)
will obey all these conditions. What multiple is it? Earlier
we saw that the square of the area of a parallelogram with
sides A and B can be written either as (A A)(
B A)(
B B)
- (A B)
- (A B)(
A B)(
A B)
or (B B)
or (B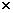 A) A) (B (B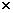 A)
. By our claim above about interchanging the dot and cross
product when we do so, applied to the first cross product
here we get : A)
. By our claim above about interchanging the dot and cross
product when we do so, applied to the first cross product
here we get :
(B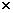 A) A) (B (B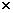 A)
= B A)
= B (A (A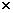 (B (B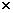 A))
=(A A))
=(A A)(
B A)(
B B)
) - (A B)
) - (A B)(
A B)(
A B) B)
If we identify A with C in A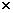 (B (B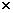 C)
and take its dot product with B we find that the multiple
consistent with this equation is 1 and we get C)
and take its dot product with B we find that the multiple
consistent with this equation is 1 and we get
A (B (B C)
= B(A C)
= B(A C)
- C(A C)
- C(A B) B)
This is sometimes called the back cab rule to remember
the appropriate signs. When applying remember that the parentheses
here are all as far back as possible in this expression
The easiest way to get the signs right is to check the
case A = i = C, B = j.
Exercise 5.5 Suppose we have a vector A in three dimensions
and an unknown vector v, but we do know A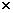 v
and A v
and A v.
Can we find v? YES! how? v.
Can we find v? YES! how?
|
