» Required Reading » Table of Contents » Chapter 6 6.2 Differentiability of Standard Functions
	Previous Section	Next Section

All of the standard functions are differentiable except at certain singular points, as follows:
Polynomials are differentiable for all arguments.
A rational function 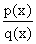is differentiable except where q(x) = 0, where the function grows to infinity. This happens in two ways, illustrated by .
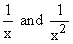Sines and cosines and exponents are differentiable everywhere but tangents and secants are singular at certain values. (where?)
The inverse functions to powers such as x^1/2 and x^1/3 are differentiable where they are defined except where the functions they are inverse to have 0 derivative.