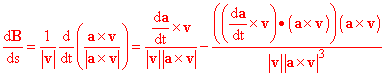» Required Reading » Table of Contents » Chapter 15 15.5 Torsion
	Previous Section	Next Chapter

We can go further. The next quantity of interest is how much the plane of curvature "twists". This is measured by the torsion of the curve, which is the magnitude of the change of the normal to the plane of curvature per unit distance at point r(t):

This derivative can easily be calculated using the fact that the direction B(t) is normal both to the tangent vector T(t) and the vector in the plane of curvature, N(t) that is normal to T(t).  We have just seen that N(t) is in the direction of the projection of a(t) normal to T(t). Since a and v are in the plane of curvature, av is normal to it, and we can write .
By the chain rule we have

.

Notice further that we can apply the product rule to the cross product to get 

and the latter term is 0.

We also have:

.

We can also use the fact that

Putting all this together  we get

We find then that the torsion is the magnitude of this and hence of the component of and divided by the area of the parallelogram formed by a and v.
Nobody remembers this formula. Be content with awareness that it exists, that you could compute it yourself if you ever were forced to do so, and that it can be set up to be calculated automatically with a spread sheet.

Exercises:

15.3 As a test of your manipulative skill, see if you can wade through the steps above yourself and get the correct answer (which may be the one given above).

15.4 Set up a spreadsheet that for a curve you input in three dimensions using a parametric representation, computes the curvature and torsion at representative values of the parameter and the coordinates of the curve point at the same values. Where is the torsion the greatest in your range?
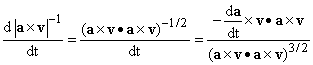