| |
|||||
There is one other tool that can sometimes be used to evaluate
anti-derivatives that works when certain convergence conditions
hold. Suppose we know the anti-derivative of g(x,a) where
g is some differentiable function of the parameter a, as well
as a function of x. Then we can deduce that an anti-derivative
of
If you cannot stand the idea of differentiating with respect to a, change a to y wherever it appears, and replace the derivative with respect to a by the partial derivative with respect to y. Then smile. |
||||||||||||||||||||||||||

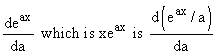 ,
and we can take higher derivatives with respect to a here
as well. This gives us a formula for an anti-derivative of
a function of the form xk eax, as
,
and we can take higher derivatives with respect to a here
as well. This gives us a formula for an anti-derivative of
a function of the form xk eax, as