|
The other important tool for anti-differentiation is one
that only indirectly concerns the subject. We know how to
anti-differentiate a function of the form (x-a)b
for any a and b. This will allow us to find the anti-derivative
of a rational function 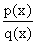 if we can reduce it to a sum of terms of that form and possibly
a polynomial instead.
if we can reduce it to a sum of terms of that form and possibly
a polynomial instead.
If p(x) has a higher degree than q(x) we can extract a quotient
polynomial s(x) by a process akin to long division called
synthetic division. We may then be left with a remainder polynomial
r(x). We know how to anti-differentiate s(x) so the task of
anti-differentiating 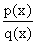 reduces to anti-differentiating
reduces to anti-differentiating 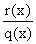 where the numerator has lower degree than the denominator.
where the numerator has lower degree than the denominator.
Suppose now that we can factor q into factors like (x-a) or
(x-b)3 or ((x-d)2+ c2)m.
The wonderful fact is that the expression 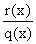 can
be separated into terms each of which has the form can
be separated into terms each of which has the form 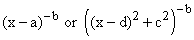 or or
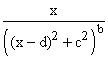 for some a's d's and c's and integer values of b, each of
which can be anti-differentiated.
for some a's d's and c's and integer values of b, each of
which can be anti-differentiated.
And here is a procedure for separating it. Suppose the denominator
q can be factored into (x-b)kt(x) such that t(b)
is not 0.
And suppose we find the first k terms of the Taylor series
expansion of 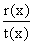 about x = b:
about x = b:
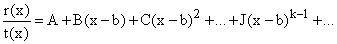
Then the terms in 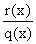 that involve inverse powers of (x-b) are given as follows:
that involve inverse powers of (x-b) are given as follows:
.
If k = 1 there is only one term, 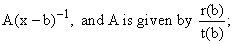
for k= 2 we have 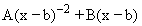 where A is as before while B is
where A is as before while B is 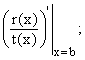 and so on.
and so on.
There are similar rules for quadratic factors.
The process of separating the denominator q in this manner
is called "the method of partial fractions".
|

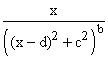 for some a's d's and c's and integer values of b, each of
which can be anti-differentiated.
for some a's d's and c's and integer values of b, each of
which can be anti-differentiated.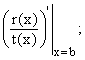 and so on.
and so on.