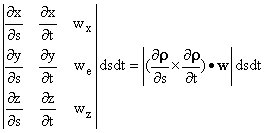» Required Reading » Table of Contents » Chapter 24 24.1 Conceptual Discussion and Main Result
	Chapter Index	Next Section

Given a surface S and vector field w, we have defined an integral, which is often called the flux of w through S. We defined it by dividing S into tiny locally planar pieces, and summing the product of the area of each piece multiplied by the component of w normal to it. This is the precise analogue of the ordinary one dimensional integral defined on an interval of the real line, with that interval replaced by our surface S. We denote it as

What then is the value of such an integral in terms of ordinary integrals?
We can answer this question directly when the surface is defined parametrically.
Suppose our surface is defined by two parameters, s and t; so that for every pair of values (s, t) in given ranges, we have values x(s, t), y(s, t) and z(s, t) which represent the coordinates of the corresponding point on S. These form a vector that we denote by
Suppose now that we make infinitesimal changes in s and t from their given values, changing s to s + ds and t to t + dt. These changes each induce changes in x, y and z, and those changes for x are respectively, x(s + ds,t) - x(s,t) and x(s,t + dt) - x(s,t), which can also be written as with similar expressions for y and z.
In short, changes in s and t induce changes in the position vector which we can denote by the vectors .
The contribution to our integral from the range of values s to s + ds and t to t + dt is the volume of the parallelepiped with base the parallelogram formed by the two vectors and with height given by the component of w normal to them.

In the drawing, A and B represent respectively.

As we saw in Chapter 3, this volume is the absolute value of the determinant whose columns are the components of the three vectors and w; which determinant can also be written according to:

This is then the answer we seek. The surface integral here can be written as the double integral over the appropriate ranges of s and t of the explicit integrand written here. In the case of ordinary integrals, we assign the positive sign to area above the x axis, and negative sign to area below it. Here we also similarly associate sign to pieces of volume, so that the integrand we normally use is the actual determinant rather than its absolute value (given above) which represents signless volume.

You will note that the sign of the expressions here is reversed on interchanging s and t, which represents the fact that on an arbitrary piece of surface there is no pre- defined answer to the question: which end is up? In whatever context you are operating, I hope you know the answer to this question, and can arrange the order of s and t here to agree with that answer.
Here then is the way a surface integral reduces to a pair of ordinary integrations:

up to the appropriate sign.

Example:

Suppose we have the surface defined by x = Rsin s cos t, y = Rsin s sin t, z = Rcos s, for 0 < s < , and 0 < t < 2and fixed parameter R. This surface is that of a sphere of radius R centered about the origin.
Suppose w is R^-2u_R which is normal to this surface, and is the electric field from a unit charge at the origin.

We find that the partials with respect to s here form the vector (Rcos s cos t, R cos s sin t, -Rsin s) while those with respect to t form (-Rsin s sin t, R sin s cos t, 0). We can evaluate the determinant by noticing that these partials are normal to each other and to w, , so that the determinant is the product of the magnitudes of these vectors, which are R, Rsin s and . Our integral becomes that of sin s ds dt and the integral becomes 4. Notice that this result is independent of R.

We also know, by the way, that the divergence of w is 0 except at the origin. This tells us, by the divergence theorem, that if we modify our surface by adding the surface of any region outside of the enclosed sphere to it, and subtracting the surface area of any region inside it that does not include the origin, we will not change this answer.
This implies that if we integrate w_b as done here over any surface (sufficiently smooth that our definitions have meaning) that bounds a region V containing the origin, we will get the same answer. It implies further that if we integrate the sum of the w's from any distribution of charges, we will get a contribution of 4 (times the sign of the charge) from each of the charges that lie inside V and none other.
This statement is called Gauss's Law. It is customary to denote the amount of charge in a small element of volume . Gauss's Law can then be written in the following form:

Exercise 24.1

Express the integral over the vertical part of the outside of a vertical cylinder of radius r from z = 0 to 1 of w_n with w = (x², xy, z²) as a pair of ordinary integrals, that is, as a multiple integral.