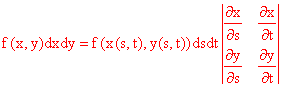» Required Reading » Table of Contents » Chapter 24 24.2 Implications for Integrals over Area in the Plane: the Jacobian
	Previous Section	Next Section

An integral over an area A in the (x, y) plane is a special and easy to visualize case of a surface integral. We can, in the results of the previous section, add the condition that z(s, t) = c throughout our surface and we have an area integral. In this case the direction normal to each element of area is always the k direction. Thus we are interested only in the z or k component of w, and that being the case can consider it to be a scalar field, that is we can set w_z = f(s, t).

The integrand multiplied by the area element in this case becomes f(s, t)dA, and if we have s = x and t = y, the area element dA is given by dxdy and this becomes f(x, y)dxdy.
The result of the previous section however, contains an important implication when s and t are not x and y. It tells you in general how to write an area integral or an integral given in terms of area element dxdy as an integral with element dsdt, if you are given any two parameters s and t for which you can write x = x(s, t) and y = y(s, t) within your given area A. In short it tells you what to do if you change variables in an area integration having area element dxdy, to get an integral over s and t with element dsdt.
And what does it tell you about this?

The "cofactor" of w_z in the determinant here is the two by two determinant which is the z component of the two by two determinant of partial derivatives of x and y with respect to s and t.

You can then deduce that the expression f(x, y)dxdy can be written as f(x(s, t),y(s, t))dsdt J, where J is called the Jacobian of the transformation from variables x, y to s, t and J is given by the absolute value of the determinant of partial derivatives of x and y with respect to s and t.

Of course we did not need to introduce the concept of a surface integral to deduce this result. When infinitesimal changes ds and dt in s and t are made, the resulting area in the xy plane is that of the parallelogram whose sides are . The area of that parallelogram is Jdsdt which is then the appropriate area element dA in terms of coordinates s and t.
This very important result is the two dimensional analogue of the chain rule, which tells us the relation between dx and ds in one dimensional integrals, .
Please remember that in this context the Jacobian defined here is always positive.

Exercises:

24.2 What is the relationship between the Jacobian going from dxdy to dsdt, and that going the opposite way?

24.3 Explain this by examining the matrix product between the matrix above and the transpose (interchange rows and columns) of the one for going the other way.

24.4 Suppose x = uv and . Find the Jacobian of this transformation.