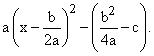» Required Reading » Table of Contents » Chapter 27 27.1 The Basic Standard Techniques
	Chapter Index	Next Section

The standard functions that we defined back in Chapter 1 include polynomials, rational functions, trigonometric functions and rational functions of these, exponentials and polynomials in these, products of exponentials and polynomials and trigonometric functions, among other things. The classes of functions mentioned above can all be integrated by standard techniques, as can some others.

We begin by reviewing the standard techniques, which have been described briefly in Chapter 19.

First, you should recognize that you can integrate any power of the variable of integration, by reversing the product rule, unless that power is -1. Thus we have

This implies that you can integrate any polynomial but also any power standing alone, even a fractional power or negative power. The result is another power except when the power integrated over is power is the -1st , whose integral is the natural logarithm, ln x, so it integrates to

Other functions that you should quickly recognize as integrable are those that are derivatives of commonly encountered functions. These include sine and cosine, the exponential function, and a few others, like

Next you should be prepared to recognize functions that can be transformed into polynomials or powers or these other functions by changes of variable of integration that are more or less suggested by the integrand. If for example, you encounter

you should think to yourself: the easy way to handle (sin x)⁷ is to make it into u⁷. And lo and behold, the rest of the integrand is du / dx so this integral becomes

.

Similarly, you should recognize

as

To handle an integral like you should recognize that a substitution will handle it. To avoid confusion, the easiest way is to set u = 3x-7 here which tells us dx = du / 3, so that the integral can be written as

Similarly you should be prepared to recognize the need for a sequence of successive simple substitutions, as in integrals like

which becomes

In doing these you are wise to write out the substitution u = u(x) completely before applying it, and make an effort not to forget to apply the chain rule in making the transition from dx to du.

With these means you can integrate any polynomial or power or any integral transformable into same by simple substitutions.

Integration by parts allows you to extend your range of doable integrals to include polynomials multiplied by exponents or by logarithms or sines and cosines, among others. It transforms an integrand into a new one with part of it integrated and the rest differentiated. Thus given a polynomial in x times (ln x) you can differentiate the latter and integrate the former, and the result will be a power that can be integrated. With an exponent or appropriate trigonometric function, times a polynomial you can differentiate the polynomial and integrate the rest, doing this repeatedly until the polynomial becomes a constant.

You can even integrate something like e^x sin x this way, by integrating by parts twice. Here are details.
First set u = e^x, dv = sin x, which gives, on integrating by parts, the new integrand -vdu which is e^x cos x. Another integration by parts similarly confronts us with the new integrand -e^x sin x and we end up with an equation for the original integral.

The same technique can be used to integrate a product of an exponential and a sine or cosine and a polynomial in x. Consider for example xe^x sin x. If we choose u = x, dv = e^x sin x, we find du = dx, v = e^x(sin x - cos x)/2, (as just shown) and the integral is reduced to a doable one.

You can integrate any polynomial in x as we have seen. You can also integrate any polynomial in sines and cosines by converting it into a sum of sines and cosines of different arguments using the expressions for them in terms of complex exponentials.
Consider for example (sin x)². We can write

A similar reduction can be made for any product of any number of sines and cosines. Any such product can be written as a sum of individual sines and cosines of arguments that are sums and differences of the arguments of the factors, in this way. This implies that you can integrate any product of a power of x of cos x of sin x and of e^kx, by applying the methods described so far.

We have already seen that we can integrate any power of x, integral or not. The method of partial fractions provides a way of taking any rational function of x, in other words, any ratio of two polynomials, and writing it as a polynomial plus a sum of inverse powers of the (x - r_j), when the denominator polynomial can be factored into linear factors and the r_j are the roots of that polynomial.

Suppose for example, our rational function is .
This function has the following obvious properties
1. when x is very large, it behaves like which is 2.
2. when x is very close to 1 it behaves like .
3. when x is very close to 2 it behaves like .
4. when x is 0 its value is .
In general such a function can be written as a polynomial plus a sum of differentiable functions divided by the most singular terms at each root. Each of the latter terms must go to zero when x is very large.
Here that means that our function can be written as

and our properties above tell us immediately
p(x) = 2, a(x) = 4, b(x) = 19 + b(x - 2), and 2 - 4 +19/4 -b/2 = -1/4, which implies b = 6, and we can write our rational function as

2 + 4(x-1)^-1 + 19(x-2)^-2 + 6(x-2)^-1

In general you can read off the coefficient of the leading singular term at each singular point by factoring that leading singular term out of the denominator, and evaluating the rest of the expression there.
If the singular term at a singular point has degree greater than 1, as the example above has at x = 2, you can find the coefficient of the non-leading terms by any of three way, whichever you find easier or more congenial to you.
1. you can factor out the leading singular factor and compute the Taylor series of the rest about the singular point. The relevant terms are those which when multiplied by the leading singular term are still singular.
2. you can subtract the leading singular term with the coefficient you have read off from the original expression; the difference will have a weaker singularity at the same point, and you can read off the coefficient of its leading term by inspection again, repeating if necessary.
3. you can evaluate the rational function at as many new points as needed to determine the unknown coefficients. That is the approach, evaluating at 0, used to determine b above.

The polynomial terms are here those that do not go to zero when x approaches infinity. The leading term can be found by inspection. The others can be determined either by polynomial division or by evaluating the polynomial coefficients using the third method described above.

If the denominator has terms that have complex roots, these may be treated exactly as real roots are.

You can extend the realm of doable integrals to rational functions of sines and cosines, by using the substitution u = tan x/2. With this substitution, we get

so that any rational function of sines and cosines becomes a rational function of u, and therefore susceptible to integration by partial fractions.

There is one other class of standardly integrable functions. These are functions that have a square root of a quadratic function in them. The quadratic function may be reduced by completing the square a form (x-a)² + b² or (x-a)²-b² or b²-(x-a)², which can be changed by changes of variable into u²+1, u²-1 and 1-u², which can be handled by substitutions involving tan x, sec x and sin x.
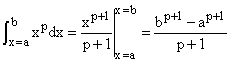
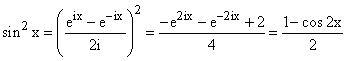
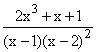Completing the square consists of rewriting the quadratic function

ax²+ bx +c

as